06.Собственные значения и собственные векторы матрицы

Пусть дана квадратная матрица N-ого порядка.

Вектор 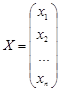называется Собственным вектором матрицы , если он обладает следующими свойствами:

Существует такое число , что

При этом называется Собственным числом (Собственным значением) матрицы

Равенство перепишем в виде

Получена система линейных однородных уравнений.

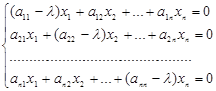
Такая система всегда имеет тривиальное (нулевое) решение. Но для того, чтобы вектор , удовлетворяющий этой системе, был собственным, необходимо, чтобы система имела ненулевое решение, т. е.

Верно и обратное: если определитель системы равен нулю, то существует собственный вектор , отвечающий данному .

Матрица

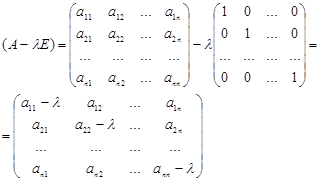
Тогда ее определитель:

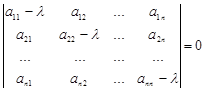
Левая часть этого равенства является многочленом N-ой степени, т. е. который называется Характеристическим многочленом матрицы , а уравнение называется Характеристическим уравнением.

Отметим, что многочлен N-ой степени имеет ровно N корней (с учетом их кратности) действительных или комплексных.

Собственные векторы действительной симметрической матрицы, соответствующие различным собственным значениям ортогональны.

Пример1. Найти собственные числа и собственные векторы матрицы

Решение. Составим характеристическое уравнение:

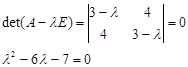
Отсюда собственные числа данной матрицы:

Найдем собственные векторы, соответствующие этим собственным значениям

Подставим собственное число в систему однородных уравнений и найдем ее нетривиальное решение.

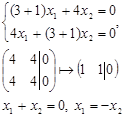
Ранг матрицы R=1, ФСР содержит (N-R)=1 решение. Пусть , тогда . Получаем собственный вектор

Рассмотрим собственное значение

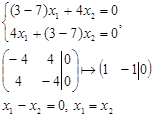
Положим , тогда . Получаем собственный вектор

Пример2. Найти собственные числа и собственные векторы матрицы

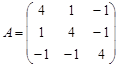
Решение. Составим характеристическое уравнение:

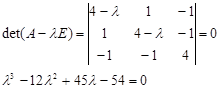
Собственные числа данной матрицы:

Найдем собственные векторы, соответствующие .

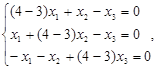
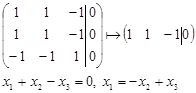
Ранг матрицы R=1, ФСР содержит (N-R)=3-1=2 решения. Зададим два набора значений свободных переменных и составим два собственных вектора

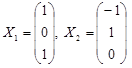
Найдем собственные векторы, соответствующие .

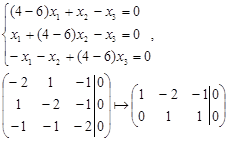
Ранг матрицы R=2, ФСР содержит (N-R)=3-1=1 решение. Зададим значение свободной переменной и составим собственный вектор

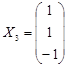
< Предыдущая		Следующая >