05.Методы решения СЛАУ. Метод обратной матрицы

Рассмотрим случай, когда число уравнений равно числу неизвестных системы:

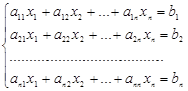(5.1)

Запишем эту систему в матричной форме:

(5.2)

Где - основная матрица системы (5.1), - столбец свободных членов, - столбец неизвестных.

Если матрица невырожденная, то существует обратная ей матрица . Домножим левосторонне равенство (5.2) На :

Таким образом, решение исходной системы имеет вид:

Пример: Найти решение системы линейных уравнений методом обратной матрицы

Решение: Выпишем основную матрицу системы и столбец свободных членов

,

Матрица, обратная к матрице системы, была найдена в §3

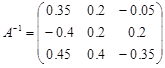
Найдем столбец неизвестных:

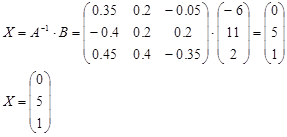
< Предыдущая		Следующая >