05.3. Однородные системы линейных уравнений. Фундаментальная система решений

Системой однородных уравнений называется система вида

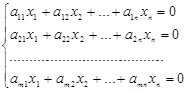
Такая система всегда совместна, т. к. имеет по крайней мере нулевое (Тривиальное) решение

Отметим, что однородная система имеет ненулевое решение тогда и только тогда, когда ранг системы меньше числа ее неизвестных, т. е.

Замечание.

1. Если число уравнений меньше числа ее неизвестных, то система имеет ненулевое решение.

2.Если число уравнений равно числу неизвестных, то система имеет ненулевое решение тогда и только тогда, когда определитель системы равен нулю.

Решения однородной системы обладают следующими свойствами:

1.Если - решение системы, то - также ее решение

2. Если - решения системы, то - также ее решение

Таким образом, из множества решений однородной системы можно выбрать базис, а любое другое ее решение может быть выражено в виде линейной комбинации решений из этого базиса.

Любой такой базис называется Фундаментальной системой решений (ФСР) однородной системы.

Отметим, что, если , то всякая ее ФСР состоит из решений.

Пример. Найти ФСР однородной системы

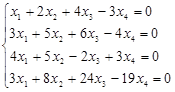
Решение. Решим систему методом Гаусса

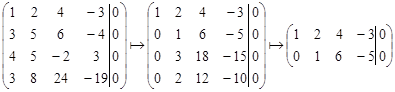Ранг матрицы R=2. Тогда ФСР состоит из решений.

Выберем в качестве свободных переменных , и выразим через них базисные переменные

Зададим свободным переменным произвольные значения и составим ФСР:

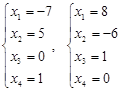
< Предыдущая		Следующая >