05.2. Метод Гаусса

Метод Гаусса - метод последовательного исключения переменных заключается в следующем: с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (в частности, треугольного) вида, из которой, начиная с последнего уравнения, последовательно находятся все переменные.

Удобней работать не с уравнениями системы, а с ее расширенной матрицей.

Заметим, что метод Гаусса позволяет решать не только системы, в которых число уравнений равно числу неизвестных, но и произвольные СЛАУ.

Отметим также, что метод Гаусса позволяет однозначно определить совместность системы, а, в случае совместности, найти ее решение.

Прмер1: Решить систему методом Гаусса

Решение: Составим расширенную матрицу системы и сведем ее к ступенчатому виду:

Перейдем к равносильной системе уравнений:

Подставляя во второе уравнение, найдем :

Подставим найденные и в первое уравнение и найдем

Решение системы:

Прмер2: Решить систему методом Гаусса:

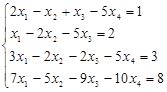
Решение: Составим расширенную матрицу системы и сведем ее к ступенчатому виду:

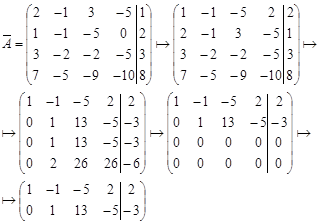
Перейдем к равносильной системе уравнений:

Выразим из последнего уравнения переменную через :

Подставим в первое уравнение системы и выразим переменную через :

Получим Общее решение исходной системы:

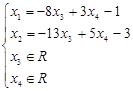
Переменные в этом случае называются Свободными, переменные - Базисными.

Задавая значения свободных переменных, можно получать так называемые Частные решения системы. Например:

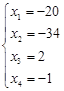
Решение системы, в котором все свободные переменные равны нулю, называется Базисным решением. Для данной системы базисное решение:

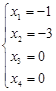
< Предыдущая		Следующая >