07.Квадратичные формы

Функция вида

Или

Где – числа, причем , называется Квадратичной формой от переменных . Числа Называются Коэффициентами квадратичной формы, а составленная из этих коэффициентов симметрическая матрица

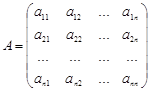- Матрицей квадратичной формы

Зная матрицу квадратичной формы, можно записать квадратичную форму в координатном виде и обратно: по данной квадратичной форме выписать ее матрицу.

Пример. Составить матрицу квадратичной формы

Решение. Выпишем коэффициенты матрицы:

(при )

(при и )

Тогда матрица квадратичной формы:

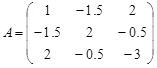
Определители

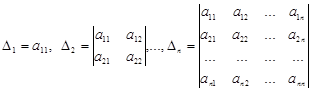
Называются Угловыми минорами матрицы .

Квадртичная форма Называется Положительно определенной (Отрицательно определенной), если для любых значений переменных , одновременно не равных нулю, она принимает положительные (отрицательные) значения, и Знакопеременной, если она принимает как положительные, так и отрицательные значения.

Пример. Квадратичная форма знакоположительна, поскольку

при всех значениях входящих в нее переменных

Квадратичная форма является знакопеременной, поскольку может принимать как положительные, так и отрицательные значения.

Не всегда по виду формы легко определить ее знак. Применяются некоторые способы. Так, например, для того, чтобы квадратичная форма была положительно определена необходимо и достаточно, чтобы все собственные числа ее матрицы были положительны. На практике чаще используют критерий Сильвестра.

Критерий Сильвестра знакоопределенности квадратичной формы:

Для того чтобы квадратичная форма

была положительно определенной, необходимо и достаточно, чтобы все угловые миноры ее матрицы были положительны:

Для того чтобы квадратичная форма

была отрицательно определенной, необходимо и достаточно, чтобы знаки главных миноров ее матрицы чередовались следующим образом

< Предыдущая		Следующая >