04.Системы линейных алгебраических уравнений (СЛАУ)
Рассмотрим систему m линейных уравнений с N неизвестными:
 (4.1)
(4.1)
![]() – неизвестные (переменные)
– неизвестные (переменные)
Числа ![]() – коэффициенты системы,
– коэффициенты системы, ![]() - свободные члены системы
- свободные члены системы
Решить систему - найти совокупность чисел ![]() подстановка которых, вместо
подстановка которых, вместо ![]() обращает уравнения в тождества.
обращает уравнения в тождества.
Система называется Совместной, если она имеет хотя бы одно решение; Несовместной, если она не имеет решений.
Совместная система, имеющая единственное, решение называется Определенной, бесчисленное множество решений – Неопределенной.
Введем обозначения:
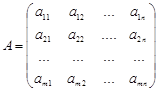 - Основная матрица системы (4.1)
- Основная матрица системы (4.1)
 - Расширенная матрица (4.1)
- Расширенная матрица (4.1)
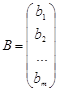 - Столбец свободных членов
- Столбец свободных членов
 - Столбец неизвестных
- Столбец неизвестных
Две системы называются Равносильными, если они имеют одно и то же множество решений. Элементарные преобразования, применяемые к строкам расширенной матрицы системы, приводят к расширенной матрице равносильной системы.
| < Предыдущая | Следующая > |
|---|