03. Обратная матрица. Ранг матрицы

Матрица называется Невырожденной, если .

Для каждой невырожденной матрицы существует единственная Обратная ей матрица, обозначаемая , такая, что

Вычисление обратной матрицы:

Где - алгебраические дополнения элементов исходной матрицы.

Пример: Найти обратную матрицу для матрицы

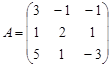
И сделать проверку

Решение: Вычислим определитель матрицы

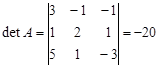
Определитель отличен от нуля, матрица невырождена, значит для нее существует обратная матрица. Найдем алгебраические дополнения элементов ее определителя:

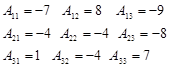
Тогда обратная матрица:

Сделаем проверку:

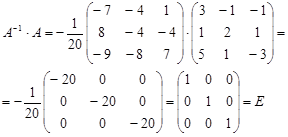
Ранг матрицы

Рассмотрим матрицу ,выделим в ней произвольным образом K Строк и K столбцов. Элементы, находящиеся на пересечении выделенных строк и столбцов, образуют квадратную матрицу K-го порядка; определитель этой матрицы является минором K-го порядка матрицы . Число миноров K-го порядка равно (). Рассмотрим всевозможные отличные от нуля миноры матрицы.

Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Пример: Методом «окаймляющих миноров» найти ранг матрицы

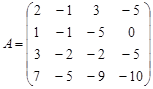
Решение: Вычислим минор четвертого порядка:

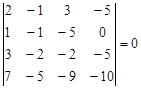
Найдем минор третьего порядка:

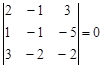
Найдем минор второго порядка:

Этот минор отличен от нуля, следовательно .

Элементарные преобразования матриц:

Изменение порядка строк (столбцов) матрицы. Отбрасывание нулевой строки (столбца) Умножение всех элементов какой-либо строки матрицы (столбца) на число, не равное нулю. Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число. Транспонирование матрицы.

Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований матрицу можно привести к трапециевидному виду (в частности к диагональному), ранг которой легко вычислить.

Пример: Найти ранг матрицы

Решение: С помощью элементарных преобразований приведем матрицу к трапециевидному виду:

Очевидно, что наивысший порядок отличного от нуля минора равен двум. Следовательно,

< Предыдущая		Следующая >