02.2. Свойства определителей

При транспонировании матрицы ее определитель не изменится. Общий множитель элементов какой-то строки (столбца), может быть вынесен за знак определителя. Если элементы одной строки (столбца) определителя соответственно равны (или пропорциональны) элементам другой строки (столбца), то определитель равен нулю. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей.

Перечисленные свойства определителей позволяют упростить вычисление определителей высших порядков. Рекомендуется преобразовать определитель так, чтобы некоторая строка (столбец) содержала как можно больше нулей, затем

Разложить его по этой строке (столбцу).

Замечание: определитель, у которого ниже (или выше) главной диагонали все элементы равны нулю, равен произведению элементов главной диагонали.

Пример: Вычислить определитель четвертого порядка

а) Разложением по элементам строки или столбца

б) Методом сведения к треугольному виду

Решение:

А) Применим свойство (2)

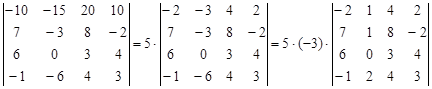Третья строка определителя содержит ноль, поэтому рационально вычислять определитель, разложив его по элементам третьей строки.

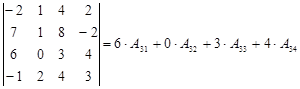
Вычислим алгебраические дополнения:

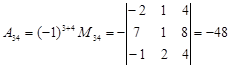
Тогда исходный определитель:

Б) Сведем исходный определитель к треугольному виду:

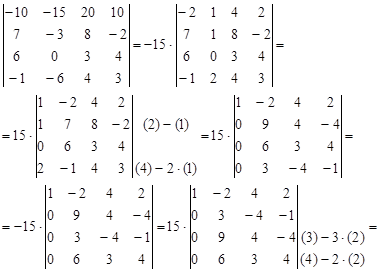
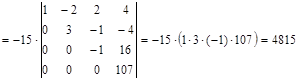
< Предыдущая		Следующая >