02. Определители

Любой квадратной матрице A N-ого порядка ставится в соответствие некоторое число, называемое Определителем N-го порядка этой матрицы (детерминантом).

Определителем N-ого порядка называется число, равное алгебраической сумме N! членов, каждый из которых является произведением N элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как , где - число инверсий в перестановке J из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания:

=

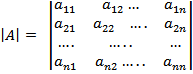Инверсии в перестановке это пары чисел, в которой большее число предшествует меньшему, например, в перестановке из трех чисел =(1,3,2) одна инверсия (3,2).

На практике вычисляют определители по другим формулам.

Определитель второго порядка равен разности произведений элементов главной и побочной диагоналей.

Пример:

Определитель третьего порядка вычисляется по формуле:

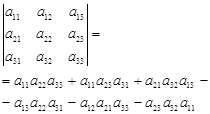
Схема вычисления (Правило треугольника):

«+» «-»

Пример:

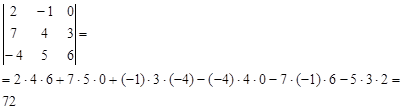
< Предыдущая		Следующая >