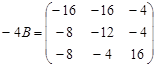01.1. Операции над матрицами
Транспонирование - замена строк на ее столбцы с сохранением их порядка (или наоборот)
 и матрицы
и матрицы  называется матрица
называется матрица 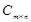 , такая, что каждый элемент
, такая, что каждый элемент 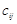 равен сумме произведений элементов I - ой строки матрицы
равен сумме произведений элементов I - ой строки матрицы 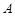 на соответствующие элементы J-ого столбца матрицы
на соответствующие элементы J-ого столбца матрицы 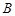
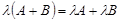
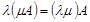

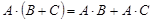
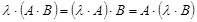
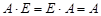 Коммутативный закон умножения, вообще говоря, не выполняется, т. е.
Коммутативный закон умножения, вообще говоря, не выполняется, т. е. 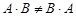
Матрицей, транспонированной к (1.1) будет являться матрица
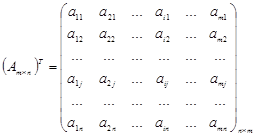
![]()
![]()
![]()
Произведение матрицы А на B существует, если число столбцов матрицы А равно числу строк матрицы В. Такие матрицы называются Согласованными.
Свойства операций над матрицами:
Пример. Вычислить матрицу ![]() , где
, где
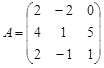 ,
, 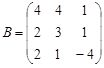

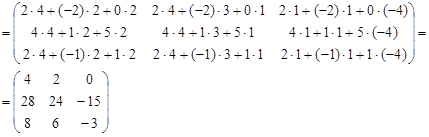
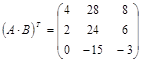
Тогда искомая матрица С:

| < Предыдущая | Следующая > |
|---|