48. Контрольное задание №1.3
1. Найти прямое произведение множеств X и Y, если: a. Х = {{a, b},c,{d, e, f}}; Y ={g, h}; b. X= {a, b, c}; Y = Ø; c. X= {2, 4, 3}; Y = {{Ø}, a, b}. 2. Найти N-ую степень множества Х, если: a. X = {x}, n=5; b. X = {a, b}, n=3; c. X = {{Ø}, y}, n=2. 3. Доказать, что для произвольных множеств X, Y, W, Z, справедливы следующие высказывания: a. (Z∪Y) × X = (Y×X)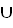 (Z×X); b. X×(Y
(Z×X); b. X×(Y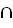 Z) = (X×Y)
Z) = (X×Y)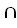 (X×Z); c. X×(Y\Z) = (X×Y)\(X×Z); d. (X×Y)
(X×Z); c. X×(Y\Z) = (X×Y)\(X×Z); d. (X×Y)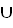 (W×Z)
(W×Z)  (X
(X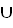 W) × (Y
W) × (Y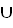 Z); e. (X∪Y) × (W
Z); e. (X∪Y) × (W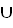 Z) = (X×W)
Z) = (X×W) 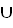 (Y×W)
(Y×W)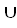 (X×Z)
(X×Z)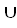 (Y×Z); 4. Для каких множеств X и Y, справедливо X ×Y=Y×X? 5. Для какого множества справедливо: А=А-1, если А
(Y×Z); 4. Для каких множеств X и Y, справедливо X ×Y=Y×X? 5. Для какого множества справедливо: А=А-1, если А Х ×Y? 6. Доказать или опровергнуть, что для множеств А и В, где А
Х ×Y? 6. Доказать или опровергнуть, что для множеств А и В, где А Х ×Y и В
Х ×Y и В Х ×Y справедливы следующие высказывания: a. Пр1(А\В) = Пр1А\Пр1В; b. Пр1(А
Х ×Y справедливы следующие высказывания: a. Пр1(А\В) = Пр1А\Пр1В; b. Пр1(А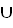 В)-1= Пр2А
В)-1= Пр2А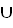 Пр2В; c. Пр1(А
Пр2В; c. Пр1(А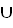 В) = Пр2А-1
В) = Пр2А-1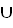 Пр2В-1; d. Пр1(А\В)-1 = Пр2А\Пр2В; e. (А
Пр2В-1; d. Пр1(А\В)-1 = Пр2А\Пр2В; e. (А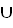 В)-1 = А-1
В)-1 = А-1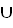 В-1; f. (А
В-1; f. (А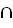 В)-1 = А-1
В)-1 = А-1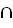 В-1; g. (А\В)-1 = А-1\В-1; 7. Доказать или опровергнуть, что для множеств А, В и С, где А
В-1; g. (А\В)-1 = А-1\В-1; 7. Доказать или опровергнуть, что для множеств А, В и С, где А Х ×Y, В
Х ×Y, В Х ×Y и С
Х ×Y и С Х ×Y справедливы следующие тождества: a. (В
Х ×Y справедливы следующие тождества: a. (В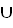 С)• А = (В • А)
С)• А = (В • А)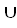 (С• А); b. А • (В\С) = (А • В)\ (А• С).
(С• А); b. А • (В\С) = (А • В)\ (А• С).