49. Контрольное задание №1.4
1. Пусть заданы отношения φ, ψ, σ на множестве Х. Доказать или опровергнуть истинность следующих тождеств: a. φ • (ψ σ) = (φ • ψ)
σ) = (φ • ψ)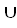 (φ • σ); b. φ
(φ • σ); b. φ 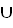 (ψ
(ψ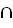 σ) = (φ
σ) = (φ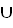 ψ)
ψ) 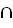 (φ
(φ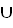 σ); c. φ • (ψ
σ); c. φ • (ψ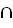 σ) = (φ • ψ)
σ) = (φ • ψ) 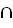 (φ • σ); d. φ
(φ • σ); d. φ 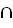 (ψ
(ψ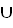 σ) = (φ
σ) = (φ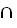 ψ)
ψ) 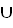 (φ
(φ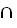 σ); 2. Проверить для произвольных отношений Ф=(A, G) и R = (A, F) справедливость утверждения: a. Если отношения Ф и R обладают свойством антирефлексивности, то отношение Ф
σ); 2. Проверить для произвольных отношений Ф=(A, G) и R = (A, F) справедливость утверждения: a. Если отношения Ф и R обладают свойством антирефлексивности, то отношение Ф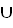 R также обладает свойством антирефлексивности. b. Если отношения Ф и R обладают свойством симметричности, то отношение Ф
R также обладает свойством антирефлексивности. b. Если отношения Ф и R обладают свойством симметричности, то отношение Ф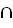 R также обладает свойством симметричности. c. Если отношения Ф и R обладают свойством транзитивности, то отношение Ф\R также обладает свойством транзитивности. d. Если отношения Ф и R обладают свойством антисимметричности, то отношение Ф-1 также обладает свойством антисимметричности. e. Если отношения Ф и R обладают свойством транзитивности, то отношение Ф • R также обладает свойством транзитивности. f. Если отношения Ф и R обладают свойством линейности, то отношение Ф\R также обладает свойством линейности. 3. Выяснить, что представляет из себя отношения Ф • Ф, Ф • Ф-1. 4. Построить на конечном множестве отношение, обладающее таким же набором свойств, что и данное отношение Ф = ({а, b, с}, {(a, b), (b, с), (с, а)}).
R также обладает свойством симметричности. c. Если отношения Ф и R обладают свойством транзитивности, то отношение Ф\R также обладает свойством транзитивности. d. Если отношения Ф и R обладают свойством антисимметричности, то отношение Ф-1 также обладает свойством антисимметричности. e. Если отношения Ф и R обладают свойством транзитивности, то отношение Ф • R также обладает свойством транзитивности. f. Если отношения Ф и R обладают свойством линейности, то отношение Ф\R также обладает свойством линейности. 3. Выяснить, что представляет из себя отношения Ф • Ф, Ф • Ф-1. 4. Построить на конечном множестве отношение, обладающее таким же набором свойств, что и данное отношение Ф = ({а, b, с}, {(a, b), (b, с), (с, а)}).