25. Задача максимизации нечеткой целевой функции на заданном нечетком множестве допустимых альтернатив
Пусть ![]() – универсальное множество альтернатив и заданы функция
– универсальное множество альтернатив и заданы функция ![]() ,
, ![]() , а также соответствующее этой функции нечеткое отображение
, а также соответствующее этой функции нечеткое отображение ![]() , где
, где ![]() – числовая ось. При этом функция
– числовая ось. При этом функция ![]() играет роль целевой и для каждого фиксированного
играет роль целевой и для каждого фиксированного ![]() задает подмножество, представляющее нечеткое описание результата выбора альтернативы
задает подмножество, представляющее нечеткое описание результата выбора альтернативы ![]() , то есть
, то есть ![]() – функция принадлежности нечеткого множества возможных значений
– функция принадлежности нечеткого множества возможных значений ![]() для
для ![]() . Пусть, кроме того, задано нечеткое множество
. Пусть, кроме того, задано нечеткое множество ![]() допустимых альтернатив с функцией принадлежности
допустимых альтернатив с функцией принадлежности ![]() .
.
Таким образом, поскольку разным альтернативам соответствуют разные значения функции принадлежности, то в этой задаче максимизации нечетко заданной целевой функции выбираемые альтернативы нужно сравнивать между собой по соответствующим им нечетким значениям функции цели. В связи с этим возникает нетривиальная проблема построения отношения предпочтения одних нечетких множеств перед другими. Эта проблема решается следующим образом.
Пусть на декартовом произведении универсальных множеств ![]() и
и ![]() задано нечеткое отношение предпочтения
задано нечеткое отношение предпочтения ![]() с функцией принадлежности
с функцией принадлежности ![]() . Эта функция задает степень уверенности в том, что элемент
. Эта функция задает степень уверенности в том, что элемент ![]() предпочтительнее элемента
предпочтительнее элемента ![]() . С другой стороны, это нечеткое отношение предпочтения можно рассматривать как нечеткое отображение элементов
. С другой стороны, это нечеткое отношение предпочтения можно рассматривать как нечеткое отображение элементов ![]() в элементы
в элементы ![]() , которые связаны с
, которые связаны с ![]() отношением
отношением ![]() , то есть
, то есть ![]() . Выберем произвольный элемент
. Выберем произвольный элемент ![]() . Образ
. Образ ![]() в
в ![]() есть нечеткое подмножество множества
есть нечеткое подмножество множества ![]() с функцией принадлежности
с функцией принадлежности ![]() , определяющей нечеткое подмножество тех элементов из
, определяющей нечеткое подмножество тех элементов из ![]() , которые связаны с
, которые связаны с ![]() отношением
отношением ![]() , то есть
, то есть ![]() .
.
Пусть теперь ![]() – нечеткое подмножество
– нечеткое подмножество ![]() . Тогда нечеткий образ
. Тогда нечеткий образ ![]() нечеткого подмножества
нечеткого подмножества ![]() при отношении
при отношении ![]() описывается функцией принадлежности
описывается функцией принадлежности
![]() , (5.45)
, (5.45)
То есть функция ![]() определяет степень предпочте-
определяет степень предпочте-
Ния нечеткого подмножества ![]() перед
перед ![]() .
.
При этом в соответствии с (5.45) для фиксированного подмножества ![]() функция
функция ![]() описывает нечеткое множество
описывает нечеткое множество ![]() элементов
элементов ![]() , связанных с
, связанных с ![]() отношением
отношением ![]() , то есть таких, что для
, то есть таких, что для ![]() ,
, ![]() имеет место
имеет место ![]() . Таким образом, функция
. Таким образом, функция ![]() устанавливает степень, с которой нечеткое множество
устанавливает степень, с которой нечеткое множество ![]() предпочтительнее элемента
предпочтительнее элемента ![]() .
.
Также несложно получить формулу для оценки степени предпочтения конкретного элемента перед нечетким множеством. Пусть ![]() – нечеткое подмножество множества
– нечеткое подмножество множества ![]() ,
, ![]() – элемент множества
– элемент множества ![]() ,
, ![]() – нечеткое отношение предпочтения с функцией принадлежности
– нечеткое отношение предпочтения с функцией принадлежности ![]() . При этом, поскольку
. При этом, поскольку ![]() можно рассматривать как отображение элементов
можно рассматривать как отображение элементов ![]() в элементы
в элементы ![]() , то
, то ![]() – есть обратное отображение элементов
– есть обратное отображение элементов ![]() в элементы
в элементы ![]() . Тогда для фиксированного
. Тогда для фиксированного ![]() функция принадлежности
функция принадлежности
![]() (5.46)
(5.46)
Определяет степень предпочтения ![]() перед
перед ![]() .
.
Пример 5.9. Пусть ![]() – числовая ось и
– числовая ось и ![]() – четкое отношение предпочтения больших чисел перед меньшими, то есть
– четкое отношение предпочтения больших чисел перед меньшими, то есть
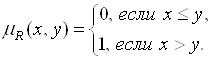
Тогда для любого ![]()
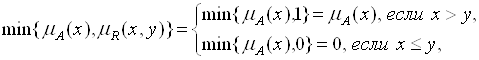
И соотношение (5.45) упрощается к виду
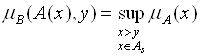 . (5.47)
. (5.47)
Зададим нечеткое множество ![]() функцией принадлежности
функцией принадлежности
(5.48), отображенной на рис. 5.14.
 (5.48)
(5.48)
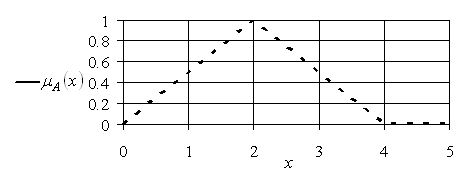
Рис. 5.14. Функция принадлежности ![]()
Пусть![]()
![]() . Тогда в соответствии с (5.47)
. Тогда в соответствии с (5.47)
![]() ,
,
То есть степень предпочтения нечеткого множества ![]() , описываемого (5.48), перед
, описываемого (5.48), перед ![]() равна
равна ![]() .
.
Пусть теперь ![]() . Тогда
. Тогда
![]()
То есть степень, с которой ![]() предпочтительнее, чем
предпочтительнее, чем ![]() , равна
, равна ![]() .
.
Определим теперь степень предпочтения конкретных элементов ![]() и
и ![]() перед нечетким множеством
перед нечетким множеством ![]() .
.
Так как
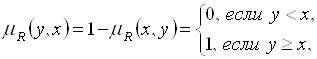
И при этом
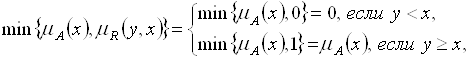
То соотношение (5.46) упростится к виду
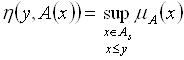 .
.
Тогда для нечеткого множества ![]() , заданного (5.48), и
, заданного (5.48), и ![]() имеем
имеем
![]() .
.
Таким образом, степень предпочтения элемента ![]() перед нечетким множеством
перед нечетким множеством ![]() равна 0.25.
равна 0.25.
Вычислим теперь степень предпочтения элемента ![]() перед нечетким множеством
перед нечетким множеством ![]() . Имеем
. Имеем
![]()
Понятно, что численное значение степени предпочтения заданного нечеткого множества перед заданным числом зависит от того, как определено нечеткое отношение предпочтения ![]() .
.
Пример 5.10. Пусть Х – числовая ось и R – нечеткое отношение предпочтения больших чисел перед меньшими, задаваемое функцией принадлежности
 (5.49)
(5.49)
Пусть нечеткое множество ![]() задано соотношением (5.48). Положим
задано соотношением (5.48). Положим ![]() При этом из (5.49) следует:
При этом из (5.49) следует:
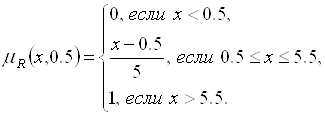
Тогда в соответствии с (5.45) имеем
![]()
На рис. 5.15 приведены графики функций принадлежности ![]()
![]()
Из рис. 5.15 следует, что функции ![]() соответствуют отрезки прямых, отображенные на этом рисунке жирно, а значение
соответствуют отрезки прямых, отображенные на этом рисунке жирно, а значение ![]() , определяющее
, определяющее ![]() , отыскивается как точка пересечения функций принадлежности
, отыскивается как точка пересечения функций принадлежности ![]() и
и ![]() .
.
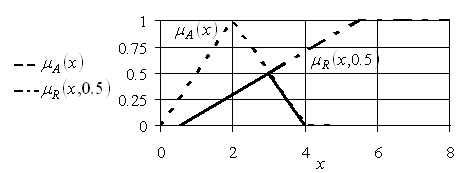
Рис. 5.15. Функции принадлежности ![]()
![]()
Решим соответствующее уравнение. Имеем
![]()
Откуда
![]()
![]() .
.
При этом
![]() ,
,
И в соответствии с (5.45)
![]() .
.
Таким образом, если отношение предпочтения задано (5.49), то степень предпочтения нечеткого множества ![]() перед 0.5 равна 0.5.
перед 0.5 равна 0.5.
Пусть теперь ![]() . При этом
. При этом 
Тогда
![]() .
.
На рис. 5.16 приведены графики функций принадлежности ![]() ,
, ![]() .
.
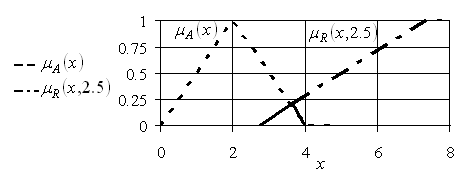
Рис. 5.16. Функции принадлежности ![]() ,
, ![]()
Действуя аналогично предыдущему, имеем
![]() ,
,
Откуда
![]() ,
, ![]() .
.
При этом
![]() .
.
Полученное значение 0.214 оценивает степень предпочтительности подмножества ![]() перед 2.5.
перед 2.5.
Введем нечеткие множества ![]() ,
, ![]() , и
, и ![]() ,
, ![]() , с функциями принадлежности
, с функциями принадлежности ![]() и
и ![]() соответственно, а также нечеткое отношение
соответственно, а также нечеткое отношение ![]() предпочтения
предпочтения ![]() перед
перед ![]() . При этом для фиксированного
. При этом для фиксированного ![]() в соответствии с (5.46) степень предпочтения
в соответствии с (5.46) степень предпочтения ![]() перед
перед ![]() рассчитывается по формуле
рассчитывается по формуле
![]() .
.
Тогда степень предпочтения множества ![]() перед множеством
перед множеством ![]() определяется соотношением
определяется соотношением
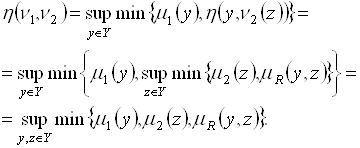 (5.50)
(5.50)
Аналогично этому легко получить оценку степени предпочтения ![]() перед
перед ![]() :
:
![]() (5.51)
(5.51)
Пример 5.11. Пусть ![]() – числовая ось и
– числовая ось и ![]() – четкое отношение пердпочтения больших чисел перед меньшими, то есть
– четкое отношение пердпочтения больших чисел перед меньшими, то есть
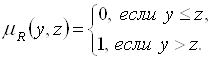
В этом случае для любых ![]() и
и ![]() соотношения (5.50) и (5.51) упростятся к виду
соотношения (5.50) и (5.51) упростятся к виду
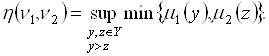 (5.52)
(5.52)
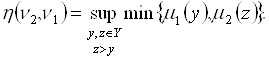 (5.53)
(5.53)
Зададим нечеткие множества ![]() и
и ![]() функции принадлежности
функции принадлежности
 (5.54)
(5.54)
 (5.54)
(5.54)
Которые отображены на рис. 5.17.
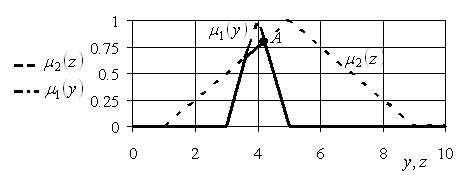
Рис. 5.17. Функции принадлежности ![]() ,
, ![]()
Тогда, в соответствии с (5.52), степень предпочтения ![]() перед
перед ![]() определяется точкой
определяется точкой ![]() на рис. 5.17, координата
на рис. 5.17, координата ![]() которой отыскивается из уравнения
которой отыскивается из уравнения
![]() ,
,
Откуда
![]() ,
, ![]() ,
, ![]() .
.
При этом степень предпочтения ![]() перед
перед ![]() равна
равна
![]() .
.
С другой стороны, в соответствии с (5.53), степень предпочтения ![]() перед
перед ![]() равна
равна ![]() , поскольку в области возможных значений пар
, поскольку в области возможных значений пар ![]() , таких, что
, таких, что ![]() , имеются
, имеются ![]() и
и ![]() , для которых
, для которых ![]() и, следовательно,
и, следовательно, ![]() .
.
Вернемся теперь к задаче максимизации нечеткой целевой функции на множестве альтернатив.
Пусть множество X допустимых альтернатив описано четко. Качество выбранной альтернативы оценивается нечеткими значениями нечеткой функции ![]() . Таким образом, любой альтернативе
. Таким образом, любой альтернативе ![]() функция
функция ![]() ставит в соответствие нечеткую оценку этой альтернативы в форме нечеткого подмножества
ставит в соответствие нечеткую оценку этой альтернативы в форме нечеткого подмножества ![]() множества оценок Y. Пусть
множества оценок Y. Пусть ![]() – степень предпочтения (соотношения (5.50), (5.51)), индуцированное некоторым нечетким отношением предпочтения
– степень предпочтения (соотношения (5.50), (5.51)), индуцированное некоторым нечетким отношением предпочтения ![]() . Как было показано, это отношение позволяет сравнить между собой по предпочтению нечеткие оценки альтернатив, а следовательно, и сами альтернативы. Другими словами, степень предпочтения альтернативы
. Как было показано, это отношение позволяет сравнить между собой по предпочтению нечеткие оценки альтернатив, а следовательно, и сами альтернативы. Другими словами, степень предпочтения альтернативы ![]() перед альтернативой
перед альтернативой ![]() определяется степенью предпочтения нечеткой оценки
определяется степенью предпочтения нечеткой оценки ![]() перед нечеткой оценкой
перед нечеткой оценкой ![]() , то есть
, то есть
![]() .
.
Для краткости обозначим через ![]() ,
, ![]() нечеткое подмножество
нечеткое подмножество ![]() значений функции
значений функции ![]() при выборе альтернативы
при выборе альтернативы ![]() и через
и через ![]() ,
, ![]() нечеткое подмножество
нечеткое подмножество ![]() значений функции
значений функции ![]() при выборе альтернативы
при выборе альтернативы ![]() . Тогда
. Тогда ![]() .
.
При этом в соответствии с (5.50), имеем
![]() . (5.56)
. (5.56)
Здесь, как уже сказано, нечеткие функции ![]() ,
, ![]() имеют смысл функций принадлежности нечетких множеств, индуцируемых функцией
имеют смысл функций принадлежности нечетких множеств, индуцируемых функцией ![]() для аргументов
для аргументов ![]() и
и ![]() .
.
Заметим, что если бы некоторая целевая функция ![]() была описана четко, то есть
была описана четко, то есть
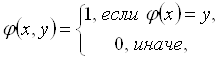
И функция предпочтения также была четкой, то есть

То (5.56) приняло бы понятный и естественный вид

Полученное соотношение (5.56) сводит задачу выбора наилучшей альтернативы к следующей. На универсальном множестве альтернатив X задано нечеткое отношение предпочтения ![]() . Теперь, с использованием методики, изложенной в п.3.6, выделим в множестве X нечеткое подмножество недоминируемых альтернатив. В соответствии с (3.39) запишем выражение для расчета степени, с которой альтернатива
. Теперь, с использованием методики, изложенной в п.3.6, выделим в множестве X нечеткое подмножество недоминируемых альтернатив. В соответствии с (3.39) запишем выражение для расчета степени, с которой альтернатива ![]() не доминируется ни одной из альтернатив множества X:
не доминируется ни одной из альтернатив множества X:
![]() . (5.57)
. (5.57)
Отсюда, с учетом (5.56), получим
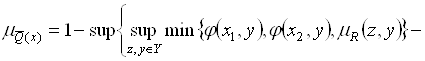
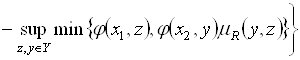 . (5.58)
. (5.58)
В простом частном случае, когда множество альтернатив задано на числовой оси с естественным предпочтением больших чисел перед меньшими, соотношение (5.56) упрощается к виду
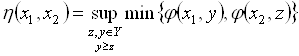 . (5.59)
. (5.59)
Аналогично этому
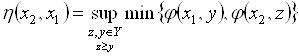 . (5.60)
. (5.60)
Понятно, что описанная методика максимизации нечеткой целевой функции на заданном нечетком множестве допустимых альтернатив может быть реализована, только если множество альтернатив конечно и содержит не слишком много элементов.
Пример 5.12. Фирма выпускает продукцию двух видов. Прибыль от реализации единицы продукции первого вида равна ![]() единиц, а от реализации продукции второго вида –
единиц, а от реализации продукции второго вида – ![]() единиц. С другой стороны, затраты на изготовление единицы продукции первого и второго видов равны соответственно
единиц. С другой стороны, затраты на изготовление единицы продукции первого и второго видов равны соответственно ![]() и
и ![]() единиц. Найти рациональную структуру производства, если суммарные затраты не должны превышать
единиц. Найти рациональную структуру производства, если суммарные затраты не должны превышать ![]() единиц.
единиц.
Введем ![]() – количество единиц продукции
– количество единиц продукции ![]() -го вида, планируемое для производства,
-го вида, планируемое для производства, ![]() .
.
Тогда сформулированная задача сводится к следующей: найти план ![]() , максимизирующий суммарную прибыль
, максимизирующий суммарную прибыль
![]() (5.61)
(5.61)
И удовлетворяющий ограничениям
![]() , (5.62)
, (5.62)
![]() ,
,![]() . (5.63)
. (5.63)
Решение этой задачи элементарно и достигается следующим образом. Введем новые переменные ![]() Тогда соотношения (5.61)–(5.63) примут вид
Тогда соотношения (5.61)–(5.63) примут вид
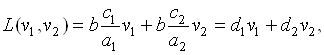 (5.64)
(5.64)
![]() (5.65)
(5.65)
![]() (5.66)
(5.66)
Оптимальное решение задачи очевидно:
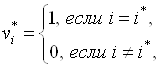 (5.67)
(5.67)
Где
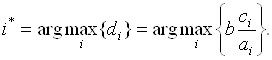 (5.68)
(5.68)
При этом

Таким образом, рациональное решение состоит в том, чтобы выпускать тот вид продукции, для которого максимально отношение 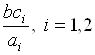 , в количестве
, в количестве ![]() единиц.
единиц.
Задача усложняется, если какие-то параметры задачи являются нечеткими числами. Пусть, например, по условию задачи прибыль от реализации единицы продукции ![]() -го вида есть нечеткое число, «Приблизительно равное
-го вида есть нечеткое число, «Приблизительно равное ![]() », с функцией принадлежности
», с функцией принадлежности
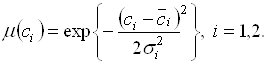 (5.69)
(5.69)
Из (5.65) следует, что структура производства однозначно задается значением одного любого элемента из пары ![]() . В связи с этим введем переменную
. В связи с этим введем переменную ![]() и запишем нечеткое значение прибыли с использованием этой переменной:
и запишем нечеткое значение прибыли с использованием этой переменной:
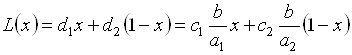 . (5.70)
. (5.70)
Теперь, с использованием (4.3) и (4.24), (4.25), получим функцию принадлежности ![]() нечеткого числа
нечеткого числа ![]() . Имеем
. Имеем
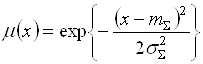 , (5.71)
, (5.71)
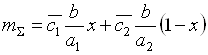 , (5.72)
, (5.72)
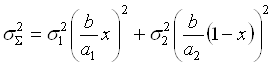 . (5.73)
. (5.73)
Дальнейшая последовательность действий такова:
А) ведем конечное множество альтернатив решения задачи;
Б) с учетом (5.71)–(5.73) рассчитаем степени предпочтения каждой из альтернатив перед другими;
В) полученную матрицу нечетких отношений предпочтения используем для отыскания недоминируемых альтернатив.
Решим задачу для следующих исходных данных: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для простоты введем универсальное множество альтернатив, содержащее всего три элемента: ![]() , то есть все средства используются для производства продукции второго вида в количестве
, то есть все средства используются для производства продукции второго вида в количестве ![]() единиц;
единиц; ![]() , то есть средства распределяются между продукцией первого вида, производимого в количестве
, то есть средства распределяются между продукцией первого вида, производимого в количестве ![]() , и продукцией второго вида, производимого в количестве
, и продукцией второго вида, производимого в количестве ![]() единиц;
единиц; ![]() , то есть все средства используются для производства продукции первого вида в количестве
, то есть все средства используются для производства продукции первого вида в количестве ![]() единиц.
единиц.
Теперь, с использованием (5.71)–(5.73), получим функции принадлежности нечетких значений прибыли, соответствующих перечисленным альтернативам:
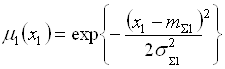 ,
, 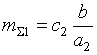 ,
, 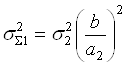 ;
;
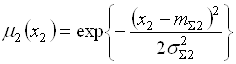 ,
,  ,
, 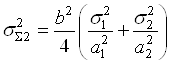 ;
;
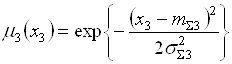 ,
, 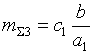 ,
,  .
.
С учетом конкретных значений параметров задачи имеем:
![]() ,
, ![]() ;
;
![]() ,
, 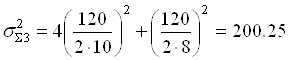 ;
;
![]() ,
, 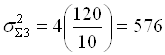 .
.
Тогда
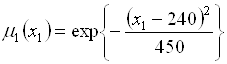 ,
, 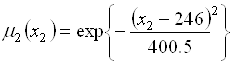 ,
,
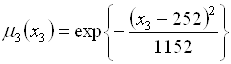 .
.
Перейдем к оценке степени предпочтения альтернатив. Поскольку оценки альтернатив заданы на числовой оси с естественным предпочтением больших чисел перед меньшими (большей прибыли перед меньшей), используем соотношение (5.59).
Найдем оценку степени предпочтения нечеткого множества с функцией принадлежности ![]() перед нечетким множеством с функцией принадлежности
перед нечетким множеством с функцией принадлежности ![]() , а также оценку степени обратного предпочтения.
, а также оценку степени обратного предпочтения.
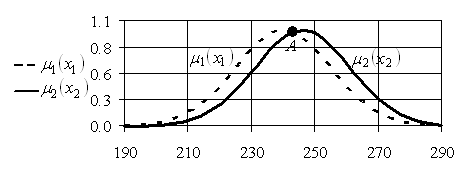
Рис. 5.18. Функции принадлежности ![]() и
и ![]()
Из графиков функций ![]() и
и ![]() , приведенных на рис. 5.18, ясно, что степень предпочтения первой альтернативы
, приведенных на рис. 5.18, ясно, что степень предпочтения первой альтернативы ![]() перед второй
перед второй ![]() определяется точкой
определяется точкой ![]() , координата которой отыскивается из уравнения
, координата которой отыскивается из уравнения
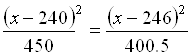 . (5.74)
. (5.74)
Из (5.74) имеем
![]() .
.
Меньший корень полученного уравнения равен ![]() . При этом степень предпочтения первой альтернативы перед второй равна
. При этом степень предпочтения первой альтернативы перед второй равна
![]() .
.
С другой стороны, в соответствии с (5.60), степень предпочтения альтернативы ![]() перед
перед ![]() равна
равна ![]() .
.
Аналогично этому найдем оценки предпочтения альтернативы ![]() перед
перед ![]() и, наоборот, альтернативы
и, наоборот, альтернативы ![]() перед
перед ![]() . Графики функций принадлежности
. Графики функций принадлежности ![]() и
и ![]() приведены на рис. 5.19.
приведены на рис. 5.19.
Уравнение для отыскания координаты точки, определяющей искомую степень предпочтения ![]() перед
перед ![]() , имеет вид
, имеет вид 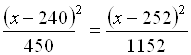 .
.
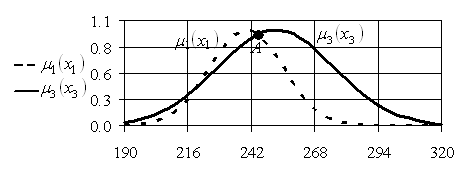
Рис. 5.19. Функции принадлежности ![]() и
и ![]()
Отсюда ![]() ,
, ![]() .
.
С другой стороны ![]() .
.
Приведем, наконец, без пояснений результаты расчета оценок предпочтения альтернативы ![]() перед
перед ![]() и альтернативы
и альтернативы ![]() перед
перед ![]() . Имеем
. Имеем
![]() ,
, ![]() .
.
Введем теперь матрицу оценок функций принадлежности для нечетких отношений предпочтения на множестве ![]() .
.
Имеем
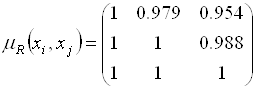 .
.
Далее
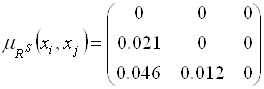 .
.
Завершая решение задачи в соответствии с методикой, изложенной в подразделе 3.6, определим степень недоминируемости каждой из альтернатив путем вычитания из единицы максимального значения в каждом из столбцов матрицы ![]() . Получим
. Получим
![]()
Наибольшую степень недоминируемости, равную ![]() , имеет альтернатива
, имеет альтернатива![]() .
.
| < Предыдущая | Следующая > |
|---|