24. Нечеткий вариант стандартной задачи математического программирования

Пусть задана следующая задача математического программирования: найти , максимизирующий целевую функцию и удовлетворяющий ограничению . Нечеткий вариант этой задачи получается, если «ослабить» ограничения, то есть допустить ту или иную степень их нарушения, и, кроме того, заменить задачу максимизации функции на близкую к ней задачу достижения некоторого заданного значения , причем различным отклонениям значений от присваивать разные степени допустимости. При этом можно задать два пороговых значения и такие, что неравенства и означают недопустимость нарушения требований к целевой функции и ограничению. Тогда можно ввести следующие нечеткие множества цели и ограничений:

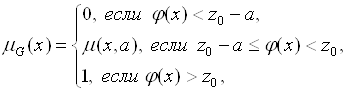(5.43)

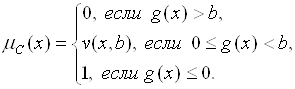(5.44)

Здесь и – некоторые функции, описывающие степень выполнения требований к целевой функции и ограничению для заданной альтернативы .

В результате исходная задача преобразована к рассмотренной выше задаче выполнения нечетко определенной цели, для решения которой применим подход Беллмана – Заде.

< Предыдущая		Следующая >