23. Задача максимизации четкой целевой функции на заданном нечетком множестве допустимых альтернатив

Пусть – универсальное множество, на котором задана четкая целевая функция и нечеткое ограничение, описываемое функцией принадлежности . Для решения соответствующей задачи математического программирования в [26] предлагается осуществить нормировку функции следующим образом:

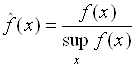(5.8)

И рассматривать далее как функцию принадлежности нечеткого множества цели лица, принимающего решение. Значение этой функции для альтернативы трактуется как степень достижения цели при выборе этой альтернативы. Теперь для решения задачи может быть применен подход Беллмана – Задe. При этом наилучшим считается выбор альтернативы, имеющей максимальную степень принадлежности нечеткому решению, то есть альтернативы , для которой достигается

Пример 5.4. На универсуме найти значение , максимизирующее целевую функцию и удовлетворяющее нечеткому ограничению – «значение должно быть близко к 6».

В соответствии с описанной технологией сначала найдем максимальное значение функции . Оно, очевидно, равно 15. Теперь осуществим нормировку целевой функции и получим

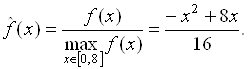
Будем рассматривать как функцию принадлежности цели. Пусть нечеткое ограничение задано функцией принадлежности

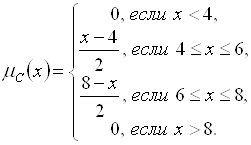
Тогда нечетким решением задачи является нечеткое множество с функцией принадлежности

Отображенное на рис. 5.6.

При этом наилучшей альтернативе соответствует значение , определяемое формулой (5.3) как решение уравнения 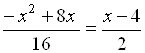. Отсюда .

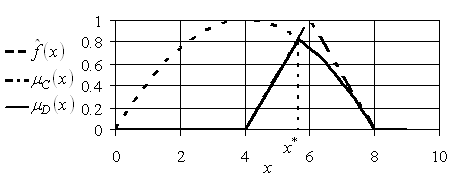
Рис. 5.6. Функции принадлежности цели, ограничения и нечеткого решения задачи

Другой подход к решению задачи максимизации четкой целевой функции на нечетком множестве допустимых альтернатив предложен в [7]. Этот подход состоит в том, что исходная задача нечеткого математического программирования сводится к совокупности обычных задач максимизации целевой функции на всевозможных множествах уровня множества допустимых альтернатив. При этом если для конкретного альтернатива есть решение задачи максимизации на множестве уровня , то это число рассматривается как степень принадлежности альтернативы нечеткому множеству решений задачи. Перебирая возможные значения , получим функцию принадлежности нечеткого решения задачи.

Рассмотрим формальную процедуру получения решения. Пусть

(5.9)

Есть множество уровня нечеткого множества альтернатив . Далее для любого введем множество

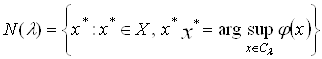. (5.10)

Понятно, что представляет собой множество решений обычной задачи максимизации целевой функции на четком множестве альтернатив, определяемом . Теперь для построения функции принадлежности нечеткого множества решений необходимо каждой альтернативе поставить в соответствие максимальное значение (точную верхнюю грань) из чисел , для которых , то есть

(5.11)

Если при этом решение задачи реализуется путем последовательного увеличения значения – степени принадлежности альтернатив нечеткому множеству, задаваемому функцией принадлежности , то для каждой альтернативы максимальное значение , для которого , естественно, равно .

Таким образом, если альтернатива принадлежит носителю нечеткого множества решений , то

. (5.12)

Формальная запись этого утверждения имеет вид

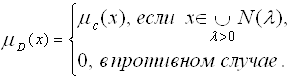(5.13)

Таким образом, решение задачи существует тогда и только тогда, когда найдется такое число , для которого .

Полученному нечеткому решению соответствует множество «максимальных» значений функции , представляющее собой образ нечеткого множества решений при отображении . Функция принадлежности нечеткого «максимального» значения функции по определению образа задается соотношением

. (5.14)

Сделаем несколько важных замечаний. Альтернатива , соответствующая максимальной степени принадлежности нечеткому множеству решений , не обязательно совпадает с альтернативой, обеспечивающей максимальную степень принадлежности нечеткому множеству ограничений . Поэтому при выборе конкретного «наилучшего» решения задачи необходимо идти на компромисс между значениями максимизируемой функции и значениями степени допустимости выбираемой альтернативы. При этом нужно учитывать, что чем больше значение целевой функции , тем меньше степень принадлежности той альтернативы , которая дает значение . Отметим, наконец, что при построении функции принадлежности нечеткого множества решений каждой альтернативе ставилось в соответствие максимальное значение , для которого максимизирует .

Из этих замечаний следует важный вывод: множество пар <значение целевой функции ; максимальное значение степени принадлежности альтернативы , обеспечивающей >, является Парето-эффективным. Альтернатива для двух функций и называется Парето-эффективной, если не существует другой альтернативы , для которой одновременно выполнялись бы неравенства и . В связи с этим увеличение значения целевой функции сопряжено со снижением степени принадлежности соответствующей альтернативы множеству допустимых альтернатив, и напротив, увеличение степени принадлежности альтернативы допустимому множеству приводит к уменьшению степени принадлежности соответствующего значения целевой функции нечеткому множеству максимальных ее значений. Этот факт легко объясним: он следует из того, что увеличение степени принадлежности альтернативы допустимому множеству сужает четкое множество значений , в пределах которого решается задача максимизации функции . При этом, естественно, максимальное значение , , не возрастает. Задача выбора наилучшей альтернативы из множества Парето-эффективных остается за лицом, принимающим решение.

Пример 5.5. Максимизировать при условии, что – нечеткое число, «Приблизительно равное четырем».

Зададим ограничение на выбор дискретным нечетким множеством с функцией принадлежности

Осуществим перебор значений в интервале с дискретностью

, отыскивая для каждого из них соответствующие множества уровня и . Имеем

, , ;

, , .

Теперь каждой альтернативе поставим в соответствие максимальное значение , для которого входит в множество значений, максимизирующих . При этом если , то ; если , то , если , то .

Таким образом, нечеткое множество решений имеет вид . Теперь, с учетом того, что , , , построим Парето-эффективное множество пар <значение целевой функции ; максимальное значение степени принадлежности альтернативы , для которой >. Это множество приведено на рис. 5.7.

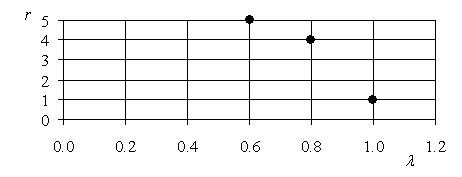
Рис. 5.7. Парето-эффективное множество решений

Аналогично решается задача в случае, когда нечеткое ограничение задано на непрерывном множестве.

Пример 5.6. Максимизировать при условии, что – нечеткое число, «Приблизительно равное четырем», с функцией принадлежности

(5.15)

В соответствии с изложенной выше методикой введем множества уровня нечеткого множества альтернатив. При этом

Множество с учетом (5.15) легко описать аналитически, решив неравенства

, .

Отсюда

. (5.16)

Теперь для формирования множества решим четкую задачу максимизации на четком множестве альтернатив (5.16). Легко видеть, что для 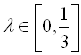максимуму соответствует .

При больших значениях в интервале этот максимум достигается на левой границе интервала . Таким образом,

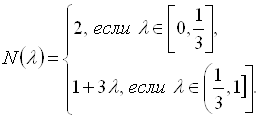(5.17)

Соотношение (5.17) для каждого устанавливает значение , максимизирующее . При этом, как ясно из (5.17), максимизирующие альтернативы лежат в интервале , то есть .

Теперь с учетом того, что каждой альтернативе следует поставить в соответствие максимальное значение , для которого входят в множество значений , максимизирующих при ограничении (5.16), опишем нечеткое множество решений функцией принадлежности

Полученному нечеткому решению соответствует нечеткое «максимальное» значение функции . Значения этого нечеткого числа зависят от и, в соответствии с (5.17), рассчитываются по формуле

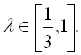, (5.18)

Функция принадлежности нечеткого «максимального» значения функции в соответствии с (5.14) имеет вид

, .

Наконец, с учетом (5.18), построим Парето-эффективное множество пар . Оно приведено на рис. 5.8.

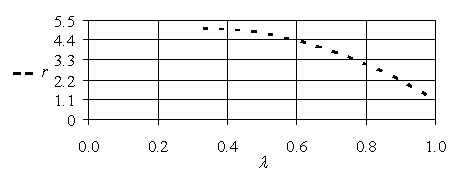
Рис. 5.8. Парето-эффективное множество решений

Из рисунка видно, что максимальное значение функции , рав-

Ное , имеет степень принадлежности множеству максимальных значений, равную .

Заметим теперь, что если ослабить ограничение (расширить интервал, соответствующий носителю нечеткой «четверки»), то это максимальное значение будет достигнуто при большем значении степени принадлежности. Например, если

То, повторяя предыдущие рассуждения, получим Парето-эффективное множество, описываемое функцией , и представленное на рис. 5.9. При этом максимальному значению функции , равному 5, соответствует степень принадлежности .

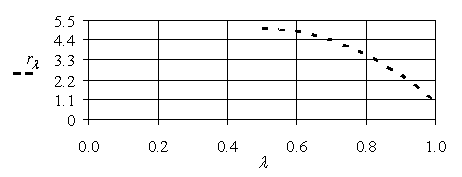
Рис. 5.9. Парето-эффективное множество пар

Описанная в примере 5.5 технология решения задачи нечеткого математического программирования, естественно, не меняется, если целевая функция зависит от многих переменных.

Пример 5.7. Минимизировать при условии, что сумма , где – нечеткое число, «Приблизительно равное трем», с функцией принадлежности

Введем множества уровня нечеткого множества альтернативных значений параметра :

(5.19)

Для расчета левой и правой границ интервала решим уравнения

Отсюда

(5.20)

Таким образом, при выбранном возникает следующая четкая задача математического программирования: найти набор , минимизирующий и удовлетворяющий ограничениям

(5.21)

(5.22)

Изобразим линии уровня функции и прямые, соответствующие ограничениям (5.21), (5.22), при , например, равном .

Положение прямых , определяется значением , однако для всех прямая, соответствующая лежит ниже прямой, соответствующей (при они обе сливаются в одну: ).

Поэтому ограничение (5.22) не является активным и минимум

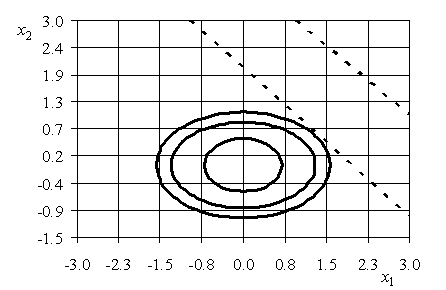
Рис. 5.10. Линии уровня и прямые ограничений

достигается в точке на прямой .

Найдем эту точку методом неопределенных множителей Лагранжа. Функция Лагранжа имеет вид

. (5.23)

Дифференцируя (5.23) по , и , получим

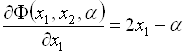, (5.24)

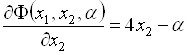, (5.25)

. (5.26)

Приравнивая полученные производные к нулю, выразим , через . Имеем

, . (5.27)

Подставив (5.27) в соотношение , найдем , откуда, с учетом (5.27),

, , . (5.28)

Соотношение (5.28) определяет множество допустимых пар , минимизирующих с заданным уровнем принадлежности . Соответствующее этому уровню принадлежности значение целевой функции равно

Парето-эффективное множество пар изображено на рис. 5.11.

Рассмотрим теперь задачу, в которой нечеткими являются коэффициенты перед переменными в ограничении.

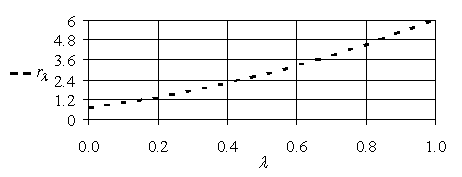
Рис. 5.11. Парето-эффективное множество пар

Пример 5.8. Минимизировать при условии, что , , , где и – нечеткие числа

(5.29)

(5.30)

В этой задаче множество уровня нечеткого множества альтернативных значений параметров и является двумерным, а его границы отыскиваются из уравнений

, , , .

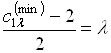Отсюда

, ; , .

Теперь при выбранном значении возникает следующая четкая задача математического программирования: найти набор , минимизирующий и удовлетворяющий ограничениям

(5.31)

Ограничения (5.31) порождают множество прямых, целиком заполняющих область, ограниченную прямыми

или , (5.32)

или , (5.33)

. (5.34)

Эта область (для ), вместе с линиями уровня функции , изображена на рис. 5.12.

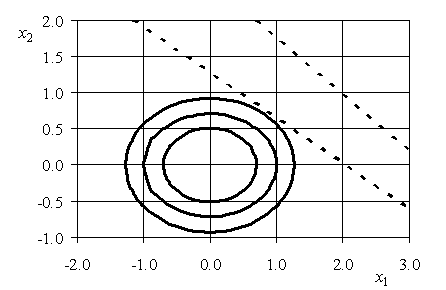
Рис. 5.12. Линии уровня и прямые ограничений

Прямые (5.32) и (5.33) максимально разнесены при . С увеличением они сближаются и при сливаются. Однако при любом прямая (5.32) лежит над прямой (5.33), поэтому в задаче минимизации ограничение (5.32) не является активным и минимум достигается в точке, лежащей на прямой (5.33). Найдем эту точку, используя метод неопределенных множителей Лагранжа. Имеем

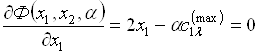, (5.35)

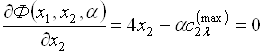, (5.36)

. (5.37)

Из (5.35) и (5.36) находим

, . (5.38)

Теперь, подставляя (5.38) в (5.37), вычислим :

Откуда

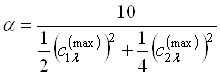Тогда

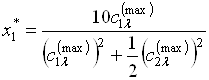, (5.39)

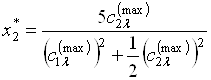. (5.40)

Далее, так как , , то

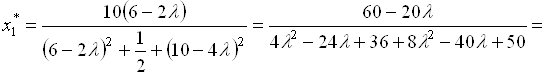
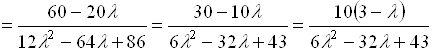. (5.41)

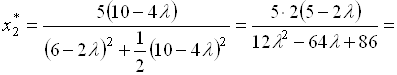
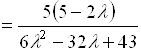. (5.42)

Соотношения (5.41), (5.42) определяют множество допустимых пар , минимизирующих с заданным уровнем принадлежности . Соответствующее этому уровню значение целевой функции :

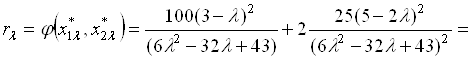
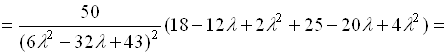
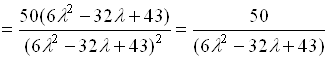Парето-эффективное множество пар Изображено на рис. 5.13.

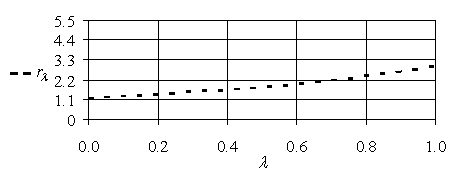
Рис. 5.13. Парето-эффективное множество пар

< Предыдущая		Следующая >