22. Задача достижения нечетко поставленной цели

По-видимому, одной из первых и наиболее простых задач нечетко-

Го математического программирования является задача достижения нечетко определенной цели, решение которой предложено Р. Беллманом и Л. Заде [29]. Это решение основано на предположении, что цель принятия решения и множество альтернатив рассматриваются как равноправные нечеткие подмножества некоторого универсального множества альтернатив. Технология получения искомого решения состоит в следующем.

Пусть – универсальное множество альтернатив, исчерпывающее совокупность всевозможных выборов лица, принимающего решение (ЛПР). Пусть далее определены нечеткая цель в и нечеткие ограничения, выделяющие из всего множества подмножество допустимых альтернатив. Нечеткая цель и нечеткие ограничения описываются функциями принадлежности и , .

Пример 5.1. Пусть – числовая ось. Нечеткая цель – «нечеткое множество чисел , больших 5», описываемое функцией принадлежности

Нечеткое ограничение – «нечеткое множество чисел , приблизительно равных 6», описываемое функцией принадлежности

.

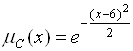При этом чем большей является степень принадлежности альтернативы нечеткому множеству цели , тем больше степень достижения цели. Аналогично этому чем большей является степень принадлежности альтернативы нечеткому множеству , тем в большей мере удовлетворяется ограничение.

Пусть некоторая альтернатива обеспечивает достижение цели со степенью и удовлетворяет ограничению со степенью . Тогда принимают, что степень принадлежности этой альтернативы искомому решению задачи равна минимальной этих величин. Таким образом, нечеткое решение задачи достижения нечеткой цели определяется пересечением нечетких множеств цели и ограничений, т. е. функция принадлежности решения имеет вид

. (5.1)

Если в задаче сформулированы несколько целей и ограничений, то нечеткое решение описывается функцией принадлежности

. (5.2)

При этом если цели и ограничения отличаются по важности и заданы соответствующие весовые коэффициенты относительной важности целей , и ограничений , , то функция принадлежности решения определяется выражением

.

Пример 5.2. Получим решение задачи для нечетко определенных цели и ограничения, описанных в примере 5.1. В соответствии с (5.1) нечетким решением задачи является нечеткое множество с функцией принадлежности

,

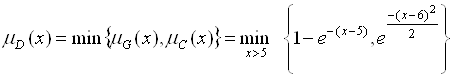Которая отображена графически на рис. 5.1.

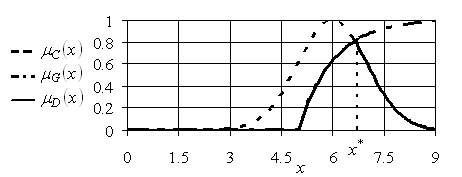
Рис. 5.1. Функции принадлежности цели, ограничения и нечеткого решения

Нечеткость полученного решения является следствием нечеткости цели и ограничения. При таком представлении решения остается неопределенность в отношении выбора наилучшей альтернативы. Наиболее естественный способ разрешения этой неопределенности состоит в выборе альтернативы , имеющей максимальную степень принадлежности нечеткому решению, т. е.

. (5.3)

Более общей является задача, в которой нечеткие цели и ограничения представляют собой подмножества разных универсальных множеств.

Пусть – универсальное множество альтернатив и пусть, кроме того, задано однозначное отображение . Значение для некоторого конкретного можно трактовать как оценку качества (эффективности) выбора этой альтернативы . При этом нечеткая цель задается в виде нечеткого подмножества множества с функцией принадлежности . Определим теперь нечеткое множество альтернатив , обеспечивающих достижение заданной цели .

Это множество представляет собой прообраз нечеткого множества при отображении , причем

. (5.4)

Понятно, что теперь задача достижения нечеткого целевого подмножества редуцирована к эквивалентной задаче достижения подмножества на множестве альтернатив, удовлетворяющих ограничениям, то есть сведена к предыдущей.

Пример 5.3. Торговая фирма продает штучный товар по цене единиц за штуку. Доход , получаемый от продажи одной единицы товара, пропорционален его цене и вероятности продажи , которая также зависит от цены, то есть . Необходимо установить цену, обеспечивающую максимальный доход.

Если зависимость выбрать в виде , то

. (5.5)

Графически зависимость (5.5) имеет вид, представленный на рис. 5.2.

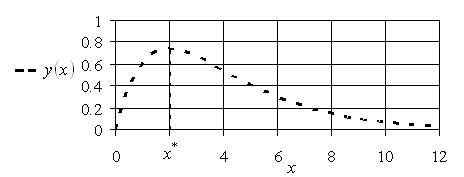
Рис. 5.2. Зависимость дохода от цены на единицу товара

Легко показать, что максимальный доход достигается при , и он равен .

Предположим, что в результате обработки ограниченного набора реальных данных об эффективности продаж получена оценка параметра . Тогда .

Поскольку в реальных условиях точная оценка параметра в (5.5) затруднительна, то цель продаж формулируется нечетко: «Получить доход, близкий к , но при этом не меньший, чем ». В соответствии с этим функцию принадлежности нечеткого целевого подмножества запишем следующим образом:

(5.6)

Пусть выбрано равным 0,6. Тогда рис. 5.3 может быть использован для отыскания оценок минимальной и максимальной цены на единицу товара. Соответствующие значения , найдем из рис. 5.3 графически. При этом интервал задает нечеткое множество альтернатив , являющееся прообразом нечеткого множества , отображающего цель продаж.

С учетом (5.4), (5.5) отыщем функцию принадлежности альтернатив для прообраза нечеткого множества цели при отображении (5.5), используя это соотношение как уравнение относительно для каждого .

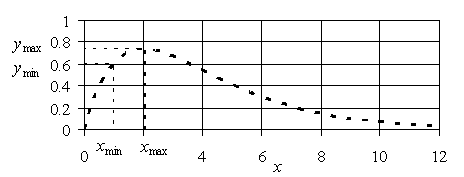
Рис. 5.3. Зависимость дохода от цены за единицу товара

Нетрудно показать, что эта функция принадлежности альтернатив для нечеткого подмножества имеет вид, приведенный на рис. 5.4.

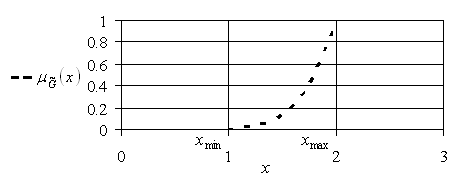
Рис. 5.4. График функции принадлежности

С другой стороны, с учетом рыночной ситуации фирма считает целесообразным ввести нечеткое ограничение на цену единицы товара: «цена X должна быть близка к середине допустимого интервала цен». Соответствующая функция принадлежности для нечеткого ограничения на значение цены может быть описана следующим образом:

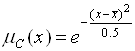, . (5.7)

Теперь задача отыскания целесообразного значения цены на единицу товара может быть решена с использованием результата пересечения нечеткого множества и нечеткого множества ограничения

. Нечеткое решение задачи отображено на рис. 5.5.

Искомое значение целесообразной цены , отыскиваемое в соответствии с (5.3), приведено на рис. 5.5.

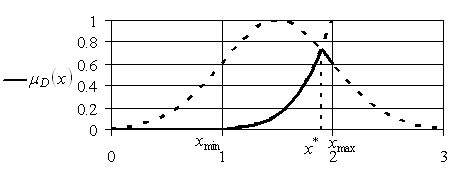
Рис. 5.5. Функции принадлежности цели, ограничения и нечеткого решения задачи

Изложенный подход к решению задачи достижения определенной цели основан на возможности симметричного описания цели и ограничений в виде нечетких подмножеств одного и того же универсального множества альтернатив. Однако этот подход может быть использован далеко не для всех задач нечеткого математического программирования. Перейдем к рассмотрению таких, более сложных задач.

< Предыдущая		Следующая >