26. Задача математического программирования, в которой параметры целевой функции и ограничений заданы нечетко
Пусть задано универсальное множество альтернатив ![]() и подмножество допустимых альтернатив, описываемое ограничениями-неравенствами вида
и подмножество допустимых альтернатив, описываемое ограничениями-неравенствами вида
![]() ,
, ![]() . (5.75)
. (5.75)
Здесь ![]() – заданные функции
– заданные функции ![]() ;
; ![]() ,
, ![]() ,
, ![]() – числовые параметры, значения которых описаны нечетко в форме подмножеств числовой оси своими функциями принадлежности
– числовые параметры, значения которых описаны нечетко в форме подмножеств числовой оси своими функциями принадлежности ![]() ,
, ![]() ,
, ![]() .
.
Эффективность каждой из возможных альтернатив оценивается значением функции цели
![]() , (5.76)
, (5.76)
В которой ![]() ,
, ![]() – числовые параметры, значения которых также описаны нечетко своими функциями принадлежности
– числовые параметры, значения которых также описаны нечетко своими функциями принадлежности ![]() ,
, ![]() . Поскольку значения целевой функции заданы на числовой оси, степень предпочтения одних альтернатив перед другими оценивается естественным предпочтением больших чисел перед меньшими.
. Поскольку значения целевой функции заданы на числовой оси, степень предпочтения одних альтернатив перед другими оценивается естественным предпочтением больших чисел перед меньшими.
Введем набор ![]() ,
, ![]() ,
, ![]() конкретных значений параметров ограничений (5.75), степени принадлежности которых определяются соответствующим набором
конкретных значений параметров ограничений (5.75), степени принадлежности которых определяются соответствующим набором ![]() ,
, ![]() ,
,![]() . Пусть
. Пусть ![]() – минимальное из этих чисел, то есть
– минимальное из этих чисел, то есть
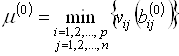 . (5.77)
. (5.77)
Если при этом некоторая конкретная альтернатива ![]() удовлетворяет неравенствам
удовлетворяет неравенствам
![]() ,
, ![]() ,
,
То естественно считать, что эта альтернатива принадлежит множеству допустимых альтернатив со степенью, не меньшей ![]() . Понятно, что полученная степень допустимости альтернативы
. Понятно, что полученная степень допустимости альтернативы ![]() может быть повышена, если найдется другой набор
может быть повышена, если найдется другой набор ![]() , удовлетворяющий ограничениям
, удовлетворяющий ограничениям ![]() ,
, ![]() ,
, ![]() ,
, ![]() , для которого значение
, для которого значение 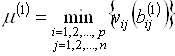
Окажется большим, чем ![]() . Отсюда следует, что истинная степень допустимости любой альтернативы
. Отсюда следует, что истинная степень допустимости любой альтернативы ![]() может быть получена из соотношения
может быть получена из соотношения
 , (5.78)
, (5.78)
Где ![]() – множество наборов
– множество наборов ![]() , таких, что
, таких, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Соотношение (5.78) задает функцию принадлежности множества допустимых альтернатив.
Пример 5.13. Пусть в задаче математического программирования подмножество допустимых альтернатив определяется неравенствами
![]() , (5.79)
, (5.79)
![]() , (5.80)
, (5.80)
Причем ![]() и
и ![]() – нечеткие параметры с функциями принадлежности
– нечеткие параметры с функциями принадлежности
 (5.81)
(5.81)
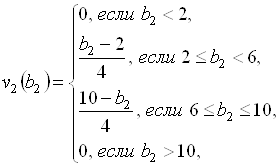 (5.82)
(5.82)
Графики которых приведены на рис. 5.20.
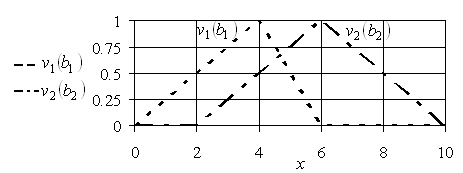
Рис. 5.20. Графики функций принадлежности ![]() ,
, ![]()
Найдем функцию принадлежности допустимых значений ![]() .
.
Сначала определим интервал значений ![]() , соответствующий носителю нечеткого числа, задающего степень допустимости альтернативы
, соответствующий носителю нечеткого числа, задающего степень допустимости альтернативы ![]() .
.
Левая граница этого интервала равна нулю, так как при минимальном возможном значении ![]() неравенства (5.79), (5.80) удовлетворяются при любых возможных значениях нечетких чисел
неравенства (5.79), (5.80) удовлетворяются при любых возможных значениях нечетких чисел ![]() и
и ![]() . При этом степень допустимости альтернативы
. При этом степень допустимости альтернативы ![]() равна 1. Действительно, при этой альтернативе неравенство (5.79) удовлетворяется, в частности, для
равна 1. Действительно, при этой альтернативе неравенство (5.79) удовлетворяется, в частности, для ![]() и
и ![]() . Поэтому
. Поэтому
![]() .
.
Далее, степень допустимости альтернатив остается равной 1 для всех тех ![]() , для которых неравенство (5.79) выполняется при условии, что нечеткие числа
, для которых неравенство (5.79) выполняется при условии, что нечеткие числа ![]() и
и ![]() принимают значения, равные модальным. Отсюда граничное значение
принимают значения, равные модальным. Отсюда граничное значение ![]() , при котором
, при котором ![]() отыскивается из уравнения
отыскивается из уравнения
![]() ,
, ![]() .
.
Таким образом,
![]() ,
, ![]() . (5.83)
. (5.83)
С другой стороны, понятно, что правая граница искомого интервала – носителя – определяется максимальным значением ![]() , при котором выполняется неравенство
, при котором выполняется неравенство
![]() ,
,
Где
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Отсюда
![]() ,
, ![]() . (5.84)
. (5.84)
Определим теперь закон изменения функции принадлежности ![]() нечеткого числа, задающего степень допустимости альтернативы
нечеткого числа, задающего степень допустимости альтернативы ![]() в интервале
в интервале ![]() . В этом интервале
. В этом интервале
![]() .
.
Пусть, например, ![]() . Тогда неравенство (5.79) принимает вид
. Тогда неравенство (5.79) принимает вид
![]() .
.
Необходимо отыскать такую пару значений ![]() и
и ![]() , чтобы выполнялось приведенное выше неравенство и одновременно значение
, чтобы выполнялось приведенное выше неравенство и одновременно значение ![]() было максимально возможным. Эту пару можно отыскать, если построить функцию принадлежности
было максимально возможным. Эту пару можно отыскать, если построить функцию принадлежности ![]() нечеткого числа
нечеткого числа ![]() и отобразить ее на одном рисунке с
и отобразить ее на одном рисунке с ![]() . В соответствии с (4.3), с учетом (5.81),
. В соответствии с (4.3), с учетом (5.81),

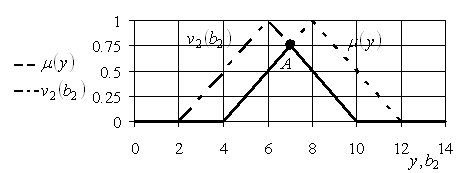
Рис. 5.21. Графики функций принадлежности ![]() ,
, ![]()
На рис. 5.21 функция ![]() отображена жирно, а значение степени допустимости выбранной альтернативы
отображена жирно, а значение степени допустимости выбранной альтернативы ![]()
![]()
Определяется точкой А пересечения ![]() и
и ![]() . При этом имеем
. При этом имеем
![]() .
.
Отсюда ![]() ,
, ![]() .
.
Это рассуждение можно повторить для произвольного значения ![]() из интервала
из интервала ![]() . При этом если
. При этом если ![]() , то соответствующая функция принадлежности примет вид
, то соответствующая функция принадлежности примет вид

Тогда точка пересечения ![]() и
и ![]() определяется из уравнения
определяется из уравнения
![]() .
.
Отсюда ![]() .
.
При этом
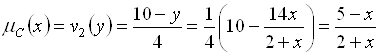 . (5.85)
. (5.85)
Полученное соотношение позволяет рассчитать степень допустимости альтернативы ![]() в интервале
в интервале ![]() . Объединяя (5.83)–(5.85), построим на рис. 5.22 график соответствующей функции принадлежности.
. Объединяя (5.83)–(5.85), построим на рис. 5.22 график соответствующей функции принадлежности.
Таким образом, искомая функция принадлежности нечеткого значения допустимости альтернативы ![]() построена.
построена.
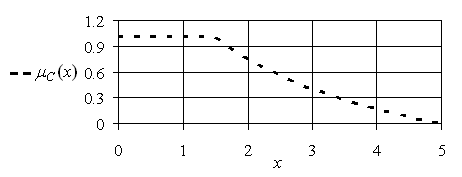
Рис. 5.22. График функции ![]()
Вернемся к нечеткой целевой функции (5.76). Пусть ![]() ,
, ![]() – конкретные числовые значения нечетких параметров функции (5.76), степени принадлежности которых соответствующим нечетким множествам определяются набором
– конкретные числовые значения нечетких параметров функции (5.76), степени принадлежности которых соответствующим нечетким множествам определяются набором ![]() ,
, ![]() . Определим теперь
. Определим теперь ![]() – минимальное из этих чисел, то есть
– минимальное из этих чисел, то есть
![]() .
.
Пусть, наконец, ![]() – некоторая конкретная альтернатива и при этом число
– некоторая конкретная альтернатива и при этом число
![]()
Есть соответствующее выбранной альтернативе ![]() и значениям параметров
и значениям параметров ![]() ,
, ![]() , значение функции цели (5.76). По аналогии с предыдущим естественно считать, что это значение
, значение функции цели (5.76). По аналогии с предыдущим естественно считать, что это значение ![]() принадлежит нечеткой (вследствие нечеткости параметров
принадлежит нечеткой (вследствие нечеткости параметров ![]() ,
, ![]() ) оценке альтернативы
) оценке альтернативы ![]() со степенью, не меньшей
со степенью, не меньшей ![]() . Понятно, что степень принадлежности
. Понятно, что степень принадлежности ![]() значения
значения ![]() функции нечеткому множеству значений функции (5.76), соответствующих альтернативе
функции нечеткому множеству значений функции (5.76), соответствующих альтернативе ![]() и равных
и равных ![]() , может быть повышена, если найдется другой набор
, может быть повышена, если найдется другой набор ![]() , для которого
, для которого
![]()
И одновременно
![]() .
.
Пример 5.14. Пусть целевая функция имеет вид
![]() ,
,
Причем параметры ![]() и
и ![]() – нечеткие числа с функциями принадлежности, соответственно равными
– нечеткие числа с функциями принадлежности, соответственно равными
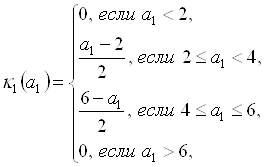 (5.86)
(5.86)
 (5.87)
(5.87)
Зададим конкретный набор значений параметров целевой функции: ![]() ,
, ![]() . Степени принадлежности выбранных значений параметров соответствующим нечетким множествам равны:
. Степени принадлежности выбранных значений параметров соответствующим нечетким множествам равны: ![]() ,
, ![]() , а значение
, а значение ![]() равно
равно 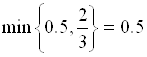 . Выберем альтернативу
. Выберем альтернативу ![]() и вычислим
и вычислим
![]() .
.
При этом значение ![]() принадлежит нечеткой оценке альтернативы
принадлежит нечеткой оценке альтернативы ![]() со степенью не ниже
со степенью не ниже ![]() . Попытаемся найти другой набор
. Попытаемся найти другой набор ![]() , для которого
, для которого
![]()
И одновременно
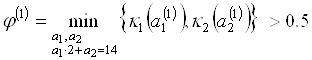 .
.
С этой целью решим следующую четкую задачу математического программирования: найти набор ![]() , максимизирующий
, максимизирующий
![]() (5.88)
(5.88)
И удовлетворяющий ограничению
![]() . (5.89)
. (5.89)
Из (5.89) выразим ![]() через
через ![]() :
:
![]() . (5.90)
. (5.90)
Подставим полученное выражение для ![]() в (5.87). При этом
в (5.87). При этом

Отсюда, после элементарных упрощений,
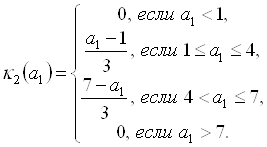 (5.91)
(5.91)
Теперь для отыскания набора, максимизирующего (5.88), отобразим функции принадлежности (5.86) и (5.91) на рис. 5.23.
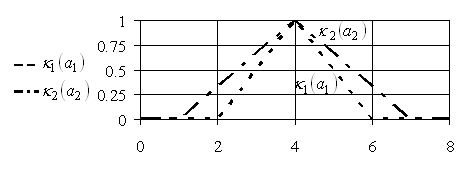
Рис. 5.23. Функции принадлежности ![]() ,
, ![]()
Из рисунка ясно, что для всех ![]() имеет место
имеет место ![]() , при-
, при-
Чем равенство достигается в точке ![]() , в которой
, в которой ![]() .
.
При этом, в соответствии с (5.89), ![]() .
.
Таким образом, найдена пара ![]() , которой соответствует максимально возможное, равное единице, значение степени принадлежности нечеткого значения
, которой соответствует максимально возможное, равное единице, значение степени принадлежности нечеткого значения ![]() функции
функции ![]() для выбранной альтернативы
для выбранной альтернативы ![]() .
.
Проведенные в примере 5.14 рассуждения можно повторить при отыскании степени принадлежности нечеткого значения ![]() функции цели, являющегося нечеткой оценкой произвольной допустимой альтернативы
функции цели, являющегося нечеткой оценкой произвольной допустимой альтернативы ![]() . Для выбранной пары
. Для выбранной пары ![]() ,
, ![]() введем множество
введем множество ![]() всех наборов
всех наборов ![]() , таких, что
, таких, что ![]() . Тогда степень принадлежности нечеткого значения
. Тогда степень принадлежности нечеткого значения ![]() , являющегося нечеткой оценкой альтернативы
, являющегося нечеткой оценкой альтернативы ![]() , имеет вид
, имеет вид
![]() , (5.92)
, (5.92)
Где
![]() ,
, ![]() , (5.93)
, (5.93)
![]() . (5.94)
. (5.94)
Понятно, что описанная технология решения нечеткой задачи математического программирования реально может быть использована только в тех случаях, когда множество альтернатив конечно и содержит не слишком много элементов.
Пример 5.15. Сформулируем нечеткую задачу линейного программирования: найти набор ![]() , максимизирующий линейную целевую функцию
, максимизирующий линейную целевую функцию
![]() (5.95)
(5.95)
И удовлетворяющий ограничениям
![]() , (5.96)
, (5.96)
![]() , (5.97)
, (5.97)
![]() ,
, ![]() , (5.98)
, (5.98)
Причем параметры целевой функции ![]() и
и ![]() – нечеткие числа с функциями принадлежности, соответственно равными
– нечеткие числа с функциями принадлежности, соответственно равными
 (5.99)
(5.99)
 (5.100)
(5.100)
Ограничения (5.96)–(5.98) высекают на плоскости ![]() выпуклый многоугольник, определяющий допустимые решения задачи. Граница области допустимых решений на рис. 5.24 выделена жирно.
выпуклый многоугольник, определяющий допустимые решения задачи. Граница области допустимых решений на рис. 5.24 выделена жирно.
На этом же рисунке помечены крайние точки многогранника ![]() , определяющие решения – опорные планы задачи. Пусть точке
, определяющие решения – опорные планы задачи. Пусть точке ![]() соответствует первая допустимая альтернатива решения –
соответствует первая допустимая альтернатива решения – ![]() , точке
, точке ![]() – вторая альтернатива
– вторая альтернатива ![]() , точке
, точке ![]() – третья альтернатива
– третья альтернатива ![]() .
.
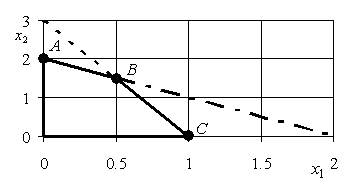
Рис. 5.24. Область допустимых решений
Из рис. 5.24 следует, что ![]() ,
, ![]() . Координаты точки
. Координаты точки ![]() найдем, решив систему уравнений
найдем, решив систему уравнений
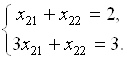
Отсюда ![]() ,
, ![]() .
.
Зададим некоторый конкретный допустимый набор значений параметров целевой функции ![]() ,
, ![]() . Степени принадлежности выбранных значений параметров соответствующим нечетким множествам равны:
. Степени принадлежности выбранных значений параметров соответствующим нечетким множествам равны: ![]() ,
, ![]() .
.
Выберем альтернативу ![]() и вычислим
и вычислим
![]() .
.
Прямая ![]() касается многоугольника ограничений в его крайней точке
касается многоугольника ограничений в его крайней точке ![]() . Поэтому альтернатива
. Поэтому альтернатива ![]() может рассматриваться как решение задачи линейного программирования с целевой функцией
может рассматриваться как решение задачи линейного программирования с целевой функцией ![]() и ограничениями (5.96)–(5.98).
и ограничениями (5.96)–(5.98).
При этом значение ![]() принадлежит нечеткой оценке альтернативы
принадлежит нечеткой оценке альтернативы ![]() со степенью, равной
со степенью, равной
![]() .
.
С целью отыскания другого возможного набора ![]() , для которого
, для которого
![]() (5.101)
(5.101)
И одновременно ![]() , решим следующую четкую задачу математического программирования: найти набор
, решим следующую четкую задачу математического программирования: найти набор ![]() , максимизирующий
, максимизирующий
![]() (5.102)
(5.102)
И удовлетворяющий ограничению ![]() .
.
В данном случае, поскольку ![]() , параметр
, параметр ![]() фиксирован, и поэтому значение критерия (5.102) не может быть улучшено.
фиксирован, и поэтому значение критерия (5.102) не может быть улучшено.
Эти же рассуждения повторим для альтернативы ![]() . Вновь выберем
. Вновь выберем ![]() ,
, ![]() и вычислим
и вычислим
![]() .
.
Прямая ![]() , проходя через крайнюю точку
, проходя через крайнюю точку ![]() многогранника ограничений, пересечет его. Поэтому альтернатива
многогранника ограничений, пересечет его. Поэтому альтернатива ![]() не является решением задачи линейного программирования с целевой функцией
не является решением задачи линейного программирования с целевой функцией ![]() и ограничениями (5.96)–(5.98).
и ограничениями (5.96)–(5.98).
В связи с этим выберем другую пару параметров целевой функции, например, ![]() ,
, ![]() . Степень принадлежности этих параметров задачи соответствующим нечетким множествам равна:
. Степень принадлежности этих параметров задачи соответствующим нечетким множествам равна: ![]() ;
; ![]() . При этом для альтернативы
. При этом для альтернативы ![]() имеем
имеем ![]() .
.
Прямая ![]() касается многогранника ограничений в крайней точке
касается многогранника ограничений в крайней точке ![]() . Поэтому альтернатива
. Поэтому альтернатива ![]() может рассматриваться как решение задачи линейного программирования с целевой функцией
может рассматриваться как решение задачи линейного программирования с целевой функцией ![]() и ограничениями (5.96)–(5.98). Значение
и ограничениями (5.96)–(5.98). Значение ![]() принадлежит нечеткой оценке альтернативы
принадлежит нечеткой оценке альтернативы ![]() со степенью, равной
со степенью, равной
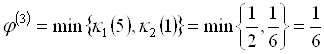 .
.
При этом, так как ![]() , параметр
, параметр ![]() фиксирован и значение степени принадлежности альтернативы
фиксирован и значение степени принадлежности альтернативы ![]() не может быть улучшено.
не может быть улучшено.
Рассмотрим, наконец, альтернативу 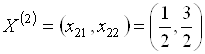 . Зададим набор значений параметров целевой функции
. Зададим набор значений параметров целевой функции ![]() ,
, ![]() со степенями принадлежности, соответствующими нечетким множествам,
со степенями принадлежности, соответствующими нечетким множествам,
Равными ![]() ,
, ![]() . Вычислим
. Вычислим
![]() .
.
Прямая ![]() касается многогранника ограничений в крайней точке
касается многогранника ограничений в крайней точке 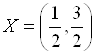 . Поэтому альтернатива
. Поэтому альтернатива 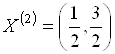 может рассматриваться как решение задачи линейного программирования с целевой функцией
может рассматриваться как решение задачи линейного программирования с целевой функцией ![]() и ограничениями (5.96)–(5.98).
и ограничениями (5.96)–(5.98).
При этом значение ![]() принадлежит нечеткой оценке альтернативы
принадлежит нечеткой оценке альтернативы 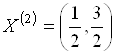 со степенью, равной
со степенью, равной
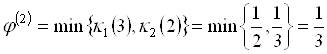 .
.
Для отыскания другого набора ![]() , для которого
, для которого
![]()
И одновременно
![]() ,
,
Решим следующую задачу математического программирования: найти набор ![]() , максимизирующий
, максимизирующий
![]() (5.103)
(5.103)
И удовлетворяющий ограничению
![]() .
.
Из этого соотношения имеем ![]() .
.
Подставим полученное выражение для ![]() в (5.99).
в (5.99).
При этом 
Отсюда, после упрощения, имеем:
 (5.104)
(5.104)
Теперь для отыскания набора, максимизирующего (5.103), отобразим функции принадлежности (5.100) и (5.104) на рис. 5.25.
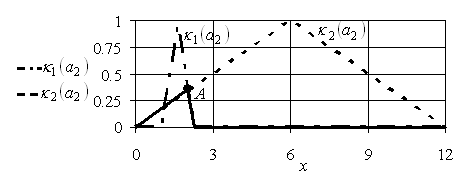
Рис. 5.25. Функции принадлежности ![]() ,
, ![]()
Из рис. 5.25 ясно, что максимальное значение функции (5.103) достигается в точке ![]() , координаты которой найдем из уравнения
, координаты которой найдем из уравнения
![]() .
.
Отсюда ![]() и
и ![]() . При этом значение
. При этом значение ![]() принадлежит нечеткой оценке альтернативы
принадлежит нечеткой оценке альтернативы 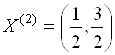 со степенью
со степенью
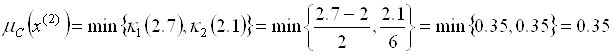 .
.
Таким образом, в результате решения задачи для допустимых альтернатив ![]() ,
, 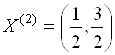 ,
, ![]() получены соответствующие значения целевой функции
получены соответствующие значения целевой функции ![]() ,
, 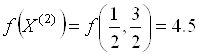 ,
, ![]() , которые принадлежат нечетким оценкам перечисленных альтернатив со степенями, равными
, которые принадлежат нечетким оценкам перечисленных альтернатив со степенями, равными ![]() ;
; ![]() ;
; ![]() .
.
Следует отметить, что описанная технология решения задачи математического программирования с нечетко заданными параметрами целевой функции и результат ее применения не вполне соответствуют интуитивно ясному представлению о том, что в действительности ожидалось получить, а именно – альтернативу, обеспечивающую наибольшее значение целевой функции с возможно большим значением степени принадлежности к нечеткому множеству, описывающему максимально возможные значения целевой функции на множестве допустимых альтернатив. Сказанное является естественным следствием конструктивных особенностей методики: произвольный выбор начального набора значений нечетких параметров целевой функции и допустимой альтернативы навязывают в такой же мере произвольное значение этой целевой функции и степень его принадлежности максимально возможному значению. Дальнейшая процедура не ориентирована на улучшение начальной альтернативы, поскольку направлена лишь на повышение степени ее принадлежности искомому решению.
В связи с этим рассмотрим другой подход к решению поставленной задачи.
Выберем некоторое число ![]() из интервала
из интервала ![]() такое, что для всех функций принадлежности нечетких параметров целевой функции выполняется неравенство
такое, что для всех функций принадлежности нечетких параметров целевой функции выполняется неравенство ![]() . Понятно [7], что в этом случае функция (5.92) обладает следующим свойством: для любого
. Понятно [7], что в этом случае функция (5.92) обладает следующим свойством: для любого ![]()
![]() .
.
Это означает, что если все нечеткие множества, описывающие нечеткие параметры целевой функции, имеют высоту, не меньшую ![]() , то для нахождения альтернатив, степень недоминируемости которых не меньше
, то для нахождения альтернатив, степень недоминируемости которых не меньше ![]() , достаточно решить следующую четкую задачу математического программирования: максимизировать функцию цели
, достаточно решить следующую четкую задачу математического программирования: максимизировать функцию цели
![]()
При ограничениях
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Следует заметить, что этот подход к решению может быть использован, если сама задача достаточно проста. Применение описанной технологии для решения общей задачи математического программирования с нечеткими параметрами сопряжено с серьезными трудностями.
Пример 5.16. Найти набор ![]() , максимизирующий линейную целевую функцию (5.95) и удовлетворяющий ограничениям (5.96)–(5.98), причем параметры целевой функции
, максимизирующий линейную целевую функцию (5.95) и удовлетворяющий ограничениям (5.96)–(5.98), причем параметры целевой функции ![]() и
и ![]() – нечеткие числа с функциями принадлежности:
– нечеткие числа с функциями принадлежности:
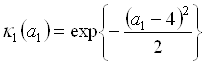 ,
, 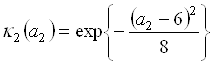 .
.
Зададим ![]() . Тогда диапазоны значений
. Тогда диапазоны значений ![]() и
и ![]() , для которых
, для которых ![]() , отыскиваются из уравнений
, отыскиваются из уравнений
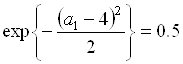 ,
, 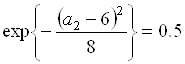 .
.
Отсюда
![]() ,
,
![]() , (5.105)
, (5.105)
![]()
![]() ,
,
![]() . (5.106)
. (5.106)
Таким образом, получена следующая четкая задача математического программирования: максимизировать (5.95) при ограничениях (5.96)–(5.98), (5.105), (5.106).
Ограничения (5.96)–(5.98) задают многоугольник, определяющий допустимые наборы ![]() (рис. 5.24). С другой стороны, ограничения (5.105), (5.106) определяют область значений нечетких параметров целевой функции
(рис. 5.24). С другой стороны, ограничения (5.105), (5.106) определяют область значений нечетких параметров целевой функции ![]() , имеющих степень принадлежности не ниже заданной (рис. 5.26).
, имеющих степень принадлежности не ниже заданной (рис. 5.26).
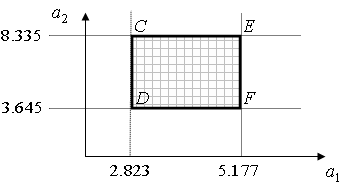
Рис. 5.26. Область значений параметров ![]() ,
, ![]() , имеющих степень принадлежности не ниже чем
, имеющих степень принадлежности не ниже чем ![]()
В полученной задаче целевая функция ![]() оказывается квадратической, а ограничения – линейные неравенства. Специфическая конструкция целевой функции позволяет свести задачу (5.95)–(5.98), (5.105), (5.106) к последовательности задач линейного программирования. С этой целью используем метод блочной релаксации [9, 15, 23].
оказывается квадратической, а ограничения – линейные неравенства. Специфическая конструкция целевой функции позволяет свести задачу (5.95)–(5.98), (5.105), (5.106) к последовательности задач линейного программирования. С этой целью используем метод блочной релаксации [9, 15, 23].
Выберем из допустимой области значений ![]() , ограниченной неравенствами (5.105), (5.106), произвольный начальный набор, например,
, ограниченной неравенствами (5.105), (5.106), произвольный начальный набор, например, ![]() ,
, ![]() . Тогда задача сведется к следующей: найти набор
. Тогда задача сведется к следующей: найти набор ![]() , максимизирующий
, максимизирующий
![]() (5.107)
(5.107)
И удовлетворяющий ограничениям (5.96)–(5.98).
Легко видеть (рис. 5.24), что максимальное значение (5.107) на множестве наборов ![]() , удовлетворяющих (5.96)–(5.98), достигается в точке
, удовлетворяющих (5.96)–(5.98), достигается в точке ![]() и равно:
и равно:
![]() .
.
Зафиксируем набор ![]() и поставим задачу отыскания
и поставим задачу отыскания ![]() , максимизирующего
, максимизирующего
![]() (5.108)
(5.108)
И удовлетворяющего ограничениям (5.105), (5.106).
Максимальное значение (5.108) достигается (рис. 5.26) в точке ![]() и равно:
и равно:
![]() .
.
Зафиксируем теперь пару ![]() и сформулируем задачу отыскания набора
и сформулируем задачу отыскания набора ![]() , максимизирующего
, максимизирующего
![]() (5.109)
(5.109)
И удовлетворяющего ограничениям (5.96)–(5.98).
Максимум (5.109) достигается (рис. 5.24) в допустимой точке ![]() и равен
и равен ![]() .
.
Дальнейшая процедура поиска пары ![]() , максимизирующей
, максимизирующей ![]() вновь приводит к набору
вновь приводит к набору ![]() ,
, ![]() .
.
Решение задачи закончено.
Контрольные вопросы
1. В чем состоит суть задач нечеткого математического программирования?
2. Каким образом применяется подход Беллмана – Заде к решению нечетких задач в различных постановках?
3. Каковы особенности первого подхода к решению задачи нечеткого математического программирования?
4. Каковы особенности второго подхода к решению задачи максимизации четкой целевой функции на нечетком множестве допустимых альтернатив?
5. Принцип решения задачи математического программирования, в которой параметры целевой функции и ограничений заданы нечетко?
| < Предыдущая |
|---|