19. Операции над нечеткими числами

Из сказанного выше понятно, что принцип обобщения может быть непосредственно использован для выполнения унарных операций над нечеткими числами.

Пусть – непрерывная, монотонная функция, – нечеткое число с функцией принадлежности . Тогда функция принадлежности образа в соответствии с (4.1), (4.2) имеет вид

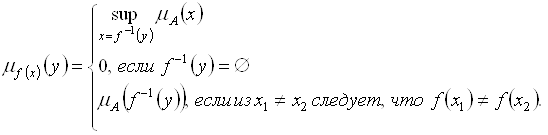(4.3)

Пример 4.4. Пусть . Тогда , .

Если, в частности, «нечеткая двойка» представлена нечетким множеством

,

То нечеткое число B, получаемое в результате применения операции и представляющее нечеткое число «минус два», записывается следующим образом:

.

Пример 4.5. Пусть , . Тогда

, .

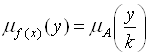Если, в частности, нечеткое множество A, представляющее «нечеткий нуль», задано функцией принадлежности , то нечеткое множество B, получаемое в результате применения операции , имеет функцию принадлежности 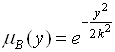. На рис. 4.2 и 4.3 приведены графики этой функции для И .

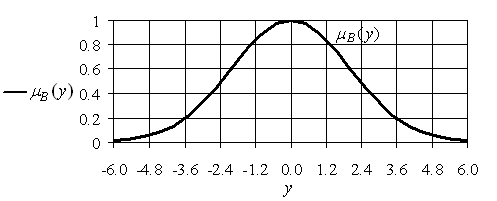
Рис. 4.2. График

Оба полученные нечеткие множества: для и , представ-

Ляют «нечеткий нуль», но с разной степенью неопределенности: в первом случае – большей, во втором – меньшей.

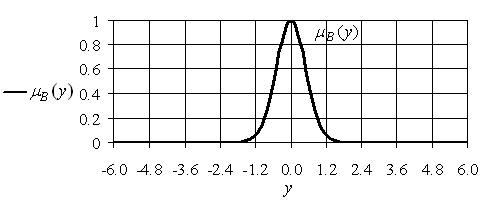
Рис. 4.3. График

Пусть теперь нечеткое множество A, представляющее «нечеткую четверку», задано функцией принадлежности

Тогда нечеткое множество B, получаемое в результате применения операции , имеет функцию принадлежности

Если, в частности, , то

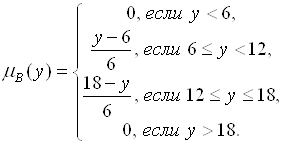
Пример 4.6. Пусть . Тогда

,

.

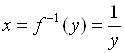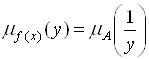Если, в частности, нечеткое множество A, представляющее «небольшое положительное число», задано функцией принадлежности , , то нечеткое множество B, получаемое в результате применения операции , имеет функцию принадлежности .

На рис. 4.4 и 4.5 приведены графики функции принадлежности и .

Нечеткое множество B представляет «Большое положительное число».

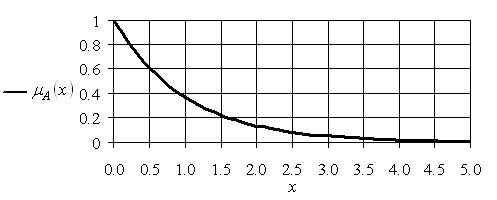
Рис. 4.4. График

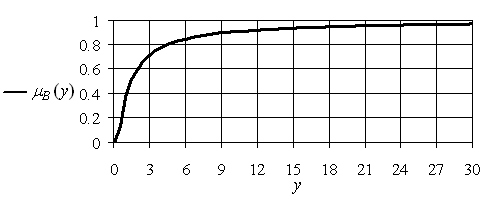
Рис. 4.5. График

Пример 4.7. Пусть , . Тогда

, .

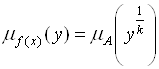Если, в частности, трапецевидное нечеткое множество А, представляющее «нечеткую четверку», задано функцией принадлежности

То нечеткое множество В, получаемое в результате применения операции , имеет функцию принадлежности

При этом нечеткое множество В для представляет «Нечеткое

Число шестнадцать», А для – «нечеткую двойку».

Пример 4.8. Пусть . Тогда

, .

Если, в частности, нечеткое множество А, представляющее «положительное число, приблизительно равное нулю», задано функцией принадлежности , , то нечеткое множество B, полученное в результате применения операции , имеет функцию принадлежности , .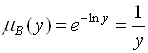

На рис. 4.6 и 4.7 приведены графики функций принадлежности и .

Рис. 4.6. График функции

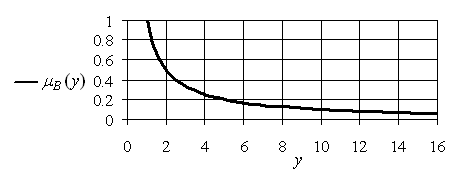
Рис. 4.7. График функции

При этом нечеткое множество В представляет «Нечеткую единицу». Понятно, что эти примеры можно продолжить.

Легкость выполнения унарных операций над нечеткими числами определяется простотой реализации. В этом случае операции , позволяющей найти значение , являющееся прообразом при отображении . Для бинарных и, вообще, -арных операций ситуация существенно усложняется. Рассмотрим, например, простейшую бинарную операцию сложения . Понятно, что некоторое значение результата сложения может быть получено бесконечным числом способов, если комбинировать произвольное значение и значение . С учетом этого обстоятельства в [10, 13] предложена иная, отличная от (4.3), форма принципа обобщения.

Пусть – набор произвольных нечетких чисел с функциями принадлежности соответственно.

Тогда функция принадлежности нечеткого числа имеет вид

. (4.4)

В простейшем частном случае сложения двух нечетких чисел и соотношение (4.4) упрощается к виду

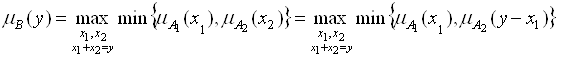. (4.5)

Пример 4.9. Пусть и – «нечеткие двойки» с функциями принадлежности

.

Найдем функцию принадлежности нечеткого числа .

Имеем

.

Таким образом,

.

Полученное нечеткое число есть «нечеткая четверка».

Таким образом, при реализации операции суммирования двух нечетких чисел и степень принадлежности конкретного значения нечеткому числу , являющемуся результатом суммирования, равна максимальной степени среди всех таких пар слагаемых, которые отображаются в одно и то же значение .

Аналогично определяются функции принадлежности чисел, являющихся результатом вычитания, умножения и деления:

,

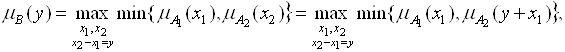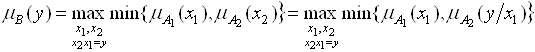, (4.6)

,,

.

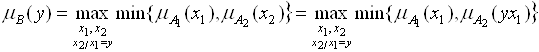Понятно, что непосредственный расчет по формулам (4.5)–(4.6) легко реализуется для нечетких чисел с дискретным носителем. Однако для непрерывных нечетких чисел непосредственное выполнение этих операций затруднено.

Дело в том, что для нечетких чисел с непрерывной функцией при-

Надлежности результат выполнения даже перечисленных простейших операций не может быть получен в общем виде, поскольку на вид функции принадлежности при описании нечетких чисел никаких ограничений не накладывается. В связи с этим в [4] описана нашедшая широкое применение аналитическая аппроксимация (форма представления) функций принадлежности нечетких чисел в виде так называемых (L-R)-функций.

Функции L-типа и R-типа. Функции (L-R)-типа определяются как произвольные невозрастающие на множестве неотрицательных действительных чисел функции, удовлетворяющие условиям

, , .

Понятно, что рассмотренные ранее треугольная функция принадлежности при и (1.14), трапециевидная функция принадлежности при и (1.15), а также -образные функции принадлежности (1.24)–(1.27) при надлежащем выборе параметров являются функциями (L-R)-типа.

Нечеткое число (L-R)-Типа. Нечетким числом (L-R)-типа Называется нечеткая величина функция принадлежности которой может быть представлена в форме композиции некоторой L-функции и некоторой R-Функции следующим образом:

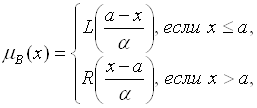(4.7)

Где α > 0 и β > 0. При этом параметр является Модой Нечеткого числа, а параметры α и β являются Левым и Правым коэффициентами нечеткости соответственно. Как ясно из этого определения, при задании нечетких чисел (L-R)-типа могут использоваться, вообще говоря, две различные функции указанного вида, что существенно расширяет диапазон их возможных представлений.

Из определения (4.7) следует, что нечеткое число (L-R)-Типа с функцией принадлежности при фиксированных L И R Функциях однозначно определяется тройкой своих параметров . Нечеткие числа (L-R)-Типа обозначаются специальным образом:.

Пример 4.10. Пусть нечеткое число (L-R)-типа задано с использованием функций

, ;, ,

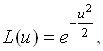
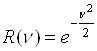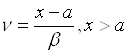Причем А = 3, α = 1, β = 2. Соответствующее нечеткое число имеет функцию принадлежности

И отображает «нечеткую тройку».

Расширением понятия нечеткого числа (L-R)-типа является понятие нечеткого интервала (L-R)-типа.

Нечеткий интервал (L-R)-типа. Нечетким интервалом (L-R)-Типа называется нечеткая величина , функция принадлежности которой может быть представлена в форме композиции некоторой L-функции и некоторой R-Функции следующим образом:

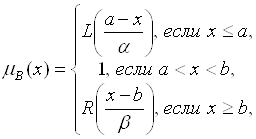
Где α > 0 и β > 0. При этом параметры A И B определяют ядро нечеткого интервала и называются соответственно Нижним и Верхним модальными значениями нечеткого интервала. Параметры α и β по-прежнему называются Левым и Правым коэффициентами нечеткости соответственно. Нечеткий интервал (L-R)-типа часто называют Толерантным Нечетким числом (L-R)-типа.

Функция принадлежности нечеткого интервала (L-R)-типа при фиксированных L И R Функциях однозначно определяется четверкой своих параметров . Нечеткие интервалы (L-R)-типа обозначаются специальным образом: . Понятно, что при A = B нечеткий интервал (L-R)-типа превращается в нечеткое число (L-R)-типа.

Пример 4.11. Зададим нечеткое число (L-R)-типа следующим образом:

График этой функции приведен на рис. 4.8.

Рис. 4.8. График функции принадлежности нечеткого числа

Пример 4.12. Зададим нечеткий интервал (L-R)-типа следующим образом:

График соответствующей функции принадлежности приведен на рис. 4.9.

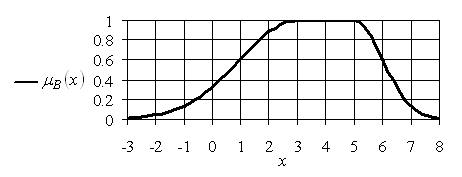
Рис. 4.9. График функции принадлежности нечеткого интервала

< Предыдущая		Следующая >