18. Нечеткие величины, числа и интервалы. Основные определения. Принцип обобщения

Принципиальное преимущество теории нечетких множеств, определяющее целесообразность ее практического применения для исследования систем, функционирующих в условиях неопределенности, основывается на возможности адекватного представления переменных таких систем с использованием этих множеств. При этом для описания переменных системы могут использоваться различные специальные нечеткие множества. Рассмотрим их.

Нечеткая величина. Нечеткой величиной называется произвольное нечеткое множество , заданное на множестве действительных чисел . Функция принадлежности нечеткой величины есть отображение . Если в качестве универсума взять подмножество неотрицательных действительных чисел , то получим определение Неотрицательной нечеткой величины .

Конкретизацией общего понятия нечеткая величина являются понятия Нечеткий интервал и нечеткое число.

Нечеткий интервал. Нечетким интервалом называется нечеткая величина с выпуклой функцией принадлежности.

Нечеткое число. Нечетким числом называется нечеткая величина, имеющая нормальную и выпуклую функцию принадлежности.

Нечеткий нуль. Нечеткое число называется Нечетким нулем, если его модальное значение равно .

Положительное (отрицательное) нечеткое число. Нечеткое число называется Положительным (отрицательным), если оно имеет строго положительный (соответственно, строго отрицательный) носитель.

Пример 4.1. Нечеткое число «нечеткая тройка» есть нечеткая вели-

Чина с функцией принадлежности, имеющей, например, вид

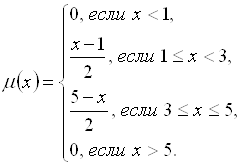
Соответствующее нечеткое множество имеет носитель – интервал [1,5] и моду, равную 3. Понятно, что нечеткое число «нечеткая тройка» может иметь множество разных, других описаний, например,

,

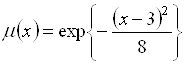Однако, во всех случаях функция принадлежности – нормальная и выпуклая функция и мода равна трем.

Введенных выше понятий недостаточно для корректного определения всего множества математических (в частности, арифметических) операций, необходимых для решения конкретных задач анализа и синтеза систем. Перейдем к рассмотрению этой проблемы.

Так как нечеткие числа и интервалы представляют собой нечеткие множества, то для них верны все свойства и выполнимы все операции, определенные ранее для нечетких множеств.

Теория нечетких множеств, в частности, нечетких чисел – шаг на пути сближения безупречной точности классической математики и всепроникающей неточности реального мира. Очевидная их несовместимость приводит к необходимости разработки комплекса понятий, методов, теории, в которых неточность воспринимается как универсальная реальность нашей жизни и которые в совокупности формирует некую полную и непротиворечивую систему правил выполнения операций над объектами этой теории, то есть алгебру. Как известно, алгебра есть раздел математики, изучающий операции над элементами множества любой природы, в частности, над числами. Алгебра – аксиоматическая теория, то есть введенные и используемые в этой теории операции определяются некоторым набором основополагающих аксиом. Этот набор может быть разным, в соответствии с этим могут быть построены разные алгебры. Все сказанное в полной мере относится к алгебрам над множеством нечетких чисел. Проведем анализ известных результатов в области построения алгебр над нечеткими числами.

При разработке алгебр над множеством нечетких чисел обычно используется так называемый принцип обобщения [4, 7, 10, 28], позволяющий перенести различные математические операции с четких множеств на нечеткие. Рассмотрим этот принцип.

Принцип обобщения представляет собой одну из фундаментальных идей теории нечетких множеств и широко используется при решении всех задач, неотъемлемым элементом которых является нечеткое отображение.

Пусть задано обычное, четкое отображение , где и – обычные конечные или бесконечные множества. Пусть далее – некоторое нечеткое подмножество множества с функцией принадлежности . Существенным и нетривиальным является вопрос о том, как построить образ нечеткого множества при отображении . Л. Заде [28] предложил следующий подход (именно он и назван принципом обобщения), результатом применения которого является отыскание образа нечеткого множества при обычном (четко описанном) отображении. В соответствии с этим принципом образ при отображении определяется как нечеткое подмножество множества , представляющее собой совокупность пар

, ,

Где – функция принадлежности образа. Понятно, что эту функцию принадлежности нечеткого множества , являющегося образом нечеткого множества при отображении , можно записать в виде

. (4.1)

Здесь множество для любого фиксированного определяется соотношением

,

То есть это множество представляет собой множество всех элементов , образом каждого из которых при отображении является элемент . Если, в частности, отображение является взаимно однозначным, то соотношение (4.1) упрощается к виду

, . (4.2)

Пример 4.2. Пусть – множество «Небольших неотрицательных целых чисел» с функцией принадлежности

, , , , ,.

Введем отображение: .

Тогда носитель нечеткого множества «Квадратов небольших неотрицательных целых чисел», являющийся носителем образа нечеткого множества при отображении , содержит набор чисел . Найдем функцию принадлежности . Так как в данном случае , то в соответствии с (4.2) имеем:

Пример 4.3. Пусть – нечеткое множество, которое представляет «Действительное число, приближенно равное двум», с функцией принадлежности

Зададим отображение: .

Тогда нечеткое множество , представляющее «Куб действительного числа, приближенно равного двум», будет иметь носитель – интервал и моду, равную 8. Найдем функцию принадлежности .

Поскольку , то в соответствии с (4.2) получим

График функции принадлежности нечеткого множества , представляющего «Куб действительного числа, приближенно равного двум», приведен на рис. 4.1.

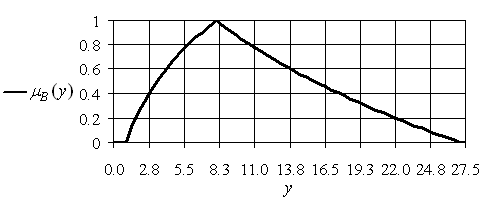
Рис. 4.1. График функции принадлежности

< Предыдущая		Следующая >