17. Нечеткие отношения предпочтения

Типичным атрибутом задач принятия решений является необходимость выбора одного из множества возможных альтернативных решений, которое лучше (или, по крайней мере, не хуже) остальных в смысле заданного отношения предпочтения. Бинарное отношение предпочтения может быть описано в виде подмножества декартова произведения множества альтернатив само на себя. Если при этом отношение предпочтения задано нечетко, то возникает ситуация, требующая специального рассмотрения.

Нечеткое отношение нестрогого предпочтения. Бинарное нечеткое отношение , заданное на декартовом произведении , называется отношением Нестрогого предпочтения, если для любой пары с некоторой степенью уверенности, равной , верно следующее утверждение: « не хуже » (обозначается таким образом: , или ). В соответствии с этим запись означает, что « не хуже », а из записи и следует, что «И не сравнимы между собой».

Отношение нестрогого предпочтения рефлексивно, то есть

при любом . Равенство означает либо то, что с положительной степенью выполняется обратное предпочтение , то есть, что , либо то, что и не сравнимы между собой ни с какой положительной степенью.

По заданному на множестве нечеткому отношению можно однозначно определить следующие соответствующие ему нечеткие отношения, используемые в задачах принятия решений для выделения наиболее предпочтительных, недоминируемых альтернатив.

Нечеткое отношение строгого предпочтения. Бинарное нечеткое отношение называется отношением Строгого Предпочтения, если для любой пары со степенью уверенности, равной , верно следующее: и не верно , то есть и одновременно . Компактная запись определения отношения имеет вид

. (3.33)

Здесь – отношение, обратное , то есть из следует, что . Запись (3.33) означает, что из всего множества пар , для которых или , удаляются те, для которых .

Если , то будем говорить, что альтернатива доминирует альтернативу . Альтернатива называется Недоминируемой, если не существует альтернативы такой, что . Отношение антирефлексивно и антисимметрично.

Функция принадлежности для пар на основании (3.33) может быть получена через функцию принадлежности :

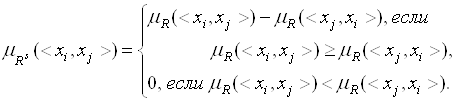(3.34)

Нечеткое отношение безразличия. Бинарное нечеткое отношение называется отношением Безразличия, если либо не выполнено ни предпочтение , ни предпочтение , либо оба эти предпочтения выполняются одновременно.

Понятно, что этому определению соответствует следующая компактная запись:

.

Отношение рефлексивно и симметрично.

Используя определения операций пересечения, объединения и дополнения над нечеткими отношениями, запишем функцию принадлежности через функцию принадлежности :

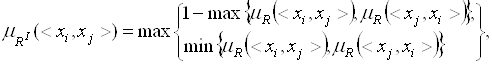(3.35)

Нечеткое отношение квазиэквивалентности. Бинарное нечеткое отношение называется отношением квазиэквивалентности, если для любой пары со степенью уверенности, определяемой функцией принадлежности , имеет место и одновременно .

Компактная запись определения отношения имеет вид:

,

А соответствующая функция принадлежности определяется соотношением

. (3.36)

Отношение рефлексивно и симметрично.

В дальнейшем, для упрощения записи, там, где это не вызывает недоразумений, будем вместо писать .

Нечеткое подмножество недоминируемых альтернатив. Рассмотрим задачу рационального выбора альтернативы из множества допустимых альтернатив , на котором задано нечеткое отношение не-

Строгого предпочтения с функцией принадлежности .

Пусть, кроме того, – соответствующее нечеткое отношение строгого предпочтения с функцией принадлежности . В соответствии с определением отношения для любой пары альтернатив величина есть степень, с которой альтернатива доминируется альтернативой . Следовательно, при фиксированном определенная на функция есть функция принадлежности нечеткого множества всех тех альтернатив , которые строго доминируются альтернативой . Понятно, что множество тех альтернатив , которые не доминируются альтернативой , может быть определено как дополнение к множеству доминируемых, причем функция принадлежности множества в соответствии с (3.16) определяется по формуле

. (3.37)

Теперь можно отыскать подмножество всех тех альтернатив , каждая из которых не доминируется ни одной из альтернатив из . Это подмножество представляет собой пересечение всех подмножеств вида по всем , то есть

.

При этом функция принадлежности для подмножества в соответствии с (3.12) определяется соотношением

. (3.38)

Значение задает степень, с которой альтернатива не доминируется ни одной из альтернатив множества .

Теперь, используя (3.34), запишем выражение (3.38) в более удобной для расчетов форме:

(3.39)

Где – функция принадлежности исходного нечеткого отношения предпочтения на множестве .

Так как величина есть степень недоминируемости альтернативы , то при выборе наилучшей альтернативы естественно отыскать ту из допустимых, которой соответствует максимальная степень принадлежности нечеткому множеству недоминируемых альтернатив.

Пример 3.23. Пусть на множестве задано нечеткое отношение предпочтения с матрицей значений функции принадлежности:

С использованием (3.34) рассчитаем матрицу значений функции принадлежности для нечеткого отношения строго предпочтения:

Теперь по формуле (3.39) определим степень недоминируемости для каждой из альтернатив, вычитая из единицы максимальное значение в каждом из столбцов матрицы .

Имеем

Наибольшую степень недоминируемости, равную , имеет альтернатива .

В рассмотренном выше подходе предполагалось, что все возмож-

Ные альтернативы в равной мере допустимы. В реальных задачах это допущение может не выполняться. В этом случае степень допустимости различных альтернатив может быть задана функцией принадлежности , . Тогда наиболее предпочтительными будут те альтернативы, которые имеют наибольшие степени недоминируемости и допустимости. Поскольку эти два качества каждой из альтернатив никак не связаны между собой, возникает необходимость компромисса, который может быть достигнут, например, следующим образом.

Пусть и , , – наборы значений степени допустимости и недоминируемости альтернатив. Тогда рациональную альтернативу предлагается отыскать из соотношения

.

Пример 3.24. Пусть

и .

Тогда

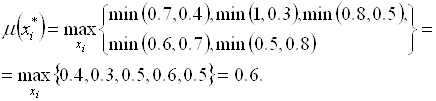
Таким образом, компромиссной альтернативой является , имеющая достаточно высокие значения степени допустимости и недоминируемости.

Контрольные вопросы

1. В чем разница между нечетким множеством и отношением?

2. Выделите основные способы задания нечетких отношений и определите их ключевые особенности.

3. Определите основные операции над нечеткими отношениями.

4. Для решения какого класса задач целесообразно использование композиции нечетких отношений?

5. Определите основные свойства нечетких отношений предпочтения, приведите примеры.

< Предыдущая		Следующая >