16. Свойства бинарных нечетких отношений, заданных на одном универсуме

Рассмотрим основные свойства бинарных нечетких отношений, которые обобщают известные свойства обычных отношений.

Рефлексивность. Бинарное нечеткое отношение , заданное на декартовом произведении , называется Рефлексивным, Если для любого из кортежей выполняется равенство:

, . (3.22)

Ясно, что все элементы главной диагонали матрицы рефлексивного бинарного нечеткого отношения с конечным универсумом равны 1.

Антирефлексивность. Бинарное нечеткое отношение , заданное на декартовом произведении , называется Антирефлексивным, Если для любого из кортежей выполняется равенство:

,. (3.23)

При этом все элементы главной диагонали матрицы антирефлексивного бинарного нечеткого отношения с конечным универсумом равны 0.

В рассмотренных в п.3.1 примерах нечеткое отношение – рефлексивно, а нечеткие отношения – антирефлекивны.

Симметричность. Бинарное нечеткое отношение , заданное на декартовом произведении , называется Симметричным, Если для любого из кортежей выполняется равенство:

, . (3.24)

Матрица симметричного бинарного нечеткого отношения с конечным универсумом симметрична относительно главной диагонали. В частности, нечеткое отношение является симметричным.

Асимметричность. Бинарное нечеткое отношение , заданное на декартовом произведении , называется Асимметричным, Если выполняется следующее условие:

, . (3.25)

Из (3.25) следует, что все элементы главной диагонали матрицы асимметричного бинарного нечеткого отношения с конечным универсумом равны 0. В дополнение к этому один из двух (а может быть? и оба) симметричных относительно главной диагонали элементов должен быть равен 0. Нечеткие отношения и являются асимметричными.

Антисимметричность. Бинарное нечеткое отношение , заданное на декартовом произведении , называется Антисимметричным, Если выполняется следующее условие:

, , (3.26)

Заметим, что антисимметричность является более слабым свойством, чем асимметричность, поскольку не требует равенства нулю элементов главной диагонали матрицы соответствующего бинарного нечеткого отношения.

Транзитивность. Бинарное нечеткое отношение , заданное на декартовом произведении , называется Транзитивным, Если выполняется следующее условие:

, .(3.27)

Нечеткое отношение является транзитивным. Этим же свойством обладает нечеткое отношение , поскольку его функция принадлежности монотонно возрастает относительно разности .

Котранзитивность. Бинарное нечеткое отношение , заданное на декартовом произведении , называется Котранзитивным, если выполняется следующее условие:

,. (3.28)

Введенные свойства симметричности (антисимметричности), рефлексивности (антирефлективности), транзитивности (котранзитивности) дают возможность разбить все типы нечетких отношений на три класса. В первый класс входят симметричные отношения, которые характеризуют сходство или различия между объектами множества . Второй класс образуют антисимметричные отношения, задающие отношения упорядоченности, доминирования. Остальные отношения входят в третий класс. Отношения каждого класса разделяются на подклассы в зависимости от выполнения условий рефлексивности и антирефлексивности.

Сходство. Бинарное нечеткое рефлексивное и симметричное отношение , заданное на декартовом произведении , называется отношением Сходства, толерантности.

Пример 3.19. Зададим в качестве универсума некоторую совокупность людей. На этом универсуме определим бинарное нечеткое отношение , описывающее условие: «человек хорошо знаком с человеком ». Ясно, что это отношение симметрично и рефлексивно.

Заметим, однако, что оно не транзитивно, поскольку из знакомства и , а также и не следует знакомство и .

Различие. Бинарное нечеткое антирефлексивное и симметричное отношение , заданное на декартовом произведении , называется отношением Различия.

Пример 3.20. Вновь в качестве универсума используем некоторую совокупность людей. Введем на универсуме бинарное нечеткое отношение, определяющее условие: «человек не равен по росту человеку ».

Это отношение, очевидно, симметрично и антирефлексивно, но так же, как и предыдущее, не транзитивно.

Эквивалентность. Бинарное нечеткое рефлексивное, симметричное и транзитивное отношение , заданное на декартовом произведении , называется отношением Эквивалентности.

Пример 3.21. На том же универсуме , представляющем некоторую совокупность людей, введем бинарное отношение, определяющее условие: «человек может непосредственно или через своих знакомых (или знакомых своих знакомых) связаться с человеком ». Это отношение рефлексивно, симметрично и транзитивно.

Нечеткое разбиение. Система нечетких подмножеств , нечеткого множества называется Нечетким разбиением, если

(3.29)

, , , , (3.30)

, , .

При этом соотношение (3.29) означает, что объединение всех (или части) нечетких подмножеств совпадает с исходным нечетким подмножеством .

Из (3.30) следует, что высота пересечения для любой пары подмножеств нечеткого разбиения строго меньше единицы.

Операция транзитивного замыкания бинарного нечеткого отношения. Рассмотрим произвольное конечное бинарное нечеткое отношение , заданное на одном базисном множестве . ОПерация транзитивного замыкания представляет собой обобщение определенной выше операции (max-min) – композиции (3.17) произвольных бинарных нечетких отношений.

Транзитивное замыкание бинарного нечеткого отношения. Транзитивным замыканием бинарного нечеткого отношения , Заданного на конечном универсуме , называется такое бинарное нечеткое отношение , которое задано на том же универсуме, а его функция принадлежности определяется следующим выражением:

, , .

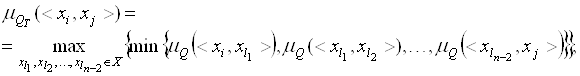
Смысл операции транзитивного замыкания бинарного нечеткого отношения можно пояснить следующим образом. Универсуму и совокупности пар , для каждой из которых определено некоторое действительное число из интервала , равное значению функции принадлежности , поставим в соответствие граф . Здесь – множество вершин графа; – множество дуг графа, которым приписаны значения функции принадлежности, определяемые вершинами начала и конца дуг. Выберем теперь пару вершин графа, например, и и построим множество всех возможных путей, начинающихся в вершине , заканчивающихся в вершине и проходящих через все остальные вершины графа. Для каждого такого пути рассчитаем некую его характеристику, задаваемую числом, равным

.

Теперь среди всех возможных путей, соединяющих вершины и , найдем такой, для которого значение характеристики будет максимальным. Повторив эту процедуру для всех пар , получим совокупность значений функции принадлежности для нечеткого отношения .

Практическое выполнение операции транзитивного замыкания бинарного нечеткого отношения реализуется с использованием представления этого отношения в форме матрицы . При этом результат операции транзитивного замыкания бинарного нечеткого отношения представляет матрица , рассчитываемая по формуле

, (3.31)

Где через обозначена -степень композиции матрицы нечеткого отношения . При этом -степень матрицы бинарного нечеткого отношения определяется рекуррентно в соответствии с выражением

. (3.32)

Таким образом, в соответствии с (3.31) совокупность -звенных путей, определяющих матрицу значений функции принадлежности для нечеткого отношения , определяется в результате объединения матриц, соответствующих однозвенным, двухзвенным, , -звенным путям. При этом следует иметь в виду, что если на каком-то, например, -м шаге вычислений матриц имеет место равенство , то, как нетрудно видеть, из этого равенства следует . Поэтому, начиная с -го шага, дальнейшие вычисления в этом случае можно прекратить.

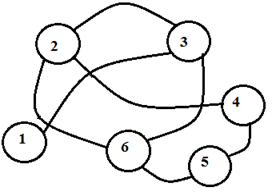
Пример 3.22. Пусть моделью некоторой локальной компьютерной сети является граф, представленный на рис. 3.2, с матрицей инциденций .

Узлы сети обладают разной пропускной способностью. В связи с этим эффективность передачи данных для разных звеньев сети не равна потенциально возможной.

Реальные значения этой эффективности можно характеризовать с использованием бинарного нечеткого отношения Q.

Рис. 3.2. Граф модели и матрица инциденций

Пусть матрица значений функции принадлежности имеет вид

.

С целью оценки эффективности передачи данных между узлами сети рассчитаем матрицу транзитивного замыкания нечеткого отношения Q. Найдем

.

Сравнение матриц и , характеризующих соответственно эффективность однозвенных и двухзвенных путей, дает возможность сделать следующие выводы.

Во-первых, с использованием двухзвенных путей появилась возможность передачи данных между узлами и , и , и , и , и , которые не связаны между собой непосредственно. Во-вторых, что гораздо важнее, для нескольких пар узлов выявлены двухзвенные пути, более надежные, чем связывающие их непосредственно однозвенные пути (например, двухзвенному пути соответствует более высокое значение функции принадлежности, чем пути ). Продолжая далее, получим

.

Так же, как и на предыдущей итерации, при расчете матрицы обнаружены трехзвенные пути, для которых степень уверенности в надежной передаче данных выше, чем для двухзвенных (например, путь эффективнее двухзвенного пути ). Кроме того, заметим, что матрица уже не содержит нулевых элементов. Это означает возможность передачи данных от любого узла сети к любому с использованием пути, длина которого не превышает трех звенев.

Выполним еще одну итерацию расчетов.

.

Анализ матрицы показывает, что с использованием четырехзвенных путей может быть повышена эффективность передачи данных между узлами и , и , и .

Рассчитаем, наконец, матрицу .

.

< Предыдущая		Следующая >