15. Отображения нечетких множеств

Пусть – некоторое нечеткое подмножество множества с функцией принадлежности .

Четкое отображение нечеткого множества. Бинарное нечеткое отношение , заданное на декартовом произведении , называется Четким отображением нечеткого множества , если для любого , , существует ровно один элемент с отличным от нуля значением функции принадлежности .

Четкая функция нечеткого множества. Если в качестве универсумов и рассматривать числовые множества, то соответствующее отображение естественно назвать Четкой функцией нечеткого множества, или Четкой функцией нечеткого аргумента.

Пусть – заданное отображение, то есть . Нечеткий образ нечеткого подмножества при отображении есть нечеткое подмножество множества , описываемое соотношением:

.

При этом функция принадлежности определяется следующим образом:

, (3.20)

.

Пример 3.16. Пусть задано нечеткое множество

.

Определим нечеткое подмножество , являющееся результатом отображения нечеткого множества . В соответствии с (3.20) имеем

.

Расширим область определения понятия отображения нечеткого множества на случай, когда каждому элементу исходного нечеткого множества при отображении ставится в соответствие не один конкретный элемент множества , а нечеткое подмножество элементов множества с функцией принадлежности, зависящей от .

Нечеткое отображение нечеткого множества. Бинарное отобра-

Жение , заданное на декартовом произведении , называется Нечетким отображением нечеткого множества , если для любого , , может быть определено нечеткое подмножество множества с функцией принадлежности , представляющей в нечеткий образ элемента при отображении .

Нечеткая функция нечеткого аргумента Представляет собой частный случай нечеткого отображения нечеткого аргумента, если и – числовые множества.

Пусть – заданная нечеткая функция, то есть . Тогда функция принадлежности для нечеткого образа нечеткого множества при нечетком отображении имеет вид

. (3.21)

Пример 3.17. Пусть задано нечеткое множество . Нечеткое отображение , определяющее нечеткие подмножества, являющиеся результатом этого отображения, введено таблицей 3.4.

Таблица 3.4. – Описание нечеткого отображения .

	Нечеткие подмножества – результат отображения
1
2

Найдем нечеткое множество , являющееся результатом нечеткого отображения нечеткого множества .

В соответствии с (3.21) имеем:

,

,

,

,

.

В этом примере результаты отображения элементов нечеткого множества заданы табличным описанием соответствующих нечетких множеств. Рассмотрим случай, когда отображение задано нечеткой функцией.

Пример 3.18. Пусть . Зададим нечеткую функцию соотношением , где – натуральное число «приблизительно равное двум», определяемое нечетким множеством .

Найдем нечеткое отображение нечеткого множества . Для упрощения понимания техники расчетов построим таблицу 3.5.

Таблица 3.5. – Исходные данные и результаты отображения

		1	2	3
		0.5	1.0	0.6
1	0.1	1	2	3
2	0.5	2	4	6
3	1.0	3	6	9

Число, находящееся в -й строке и -м столбце таблицы, представляет значение , соответствующее -му варианту отображения элемента .

Теперь, в соответствии с (3.21), определим нечеткое множество , являющееся результатом нечеткого отображения нечеткого множества .

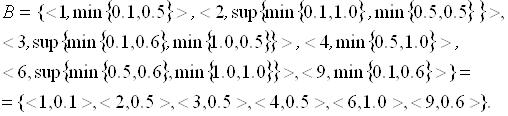
Нечеткая алгебраическая операция. Аналогичным образом вво-

Дится понятие Нечеткой алгебраической операции, Которая является частным случаем нечеткого отображения, когда все универсумы тождественно равны . При этом Нечеткая -местная операция Записывается в форме .

< Предыдущая		Следующая >