14. Композиция двух бинарных нечетких отношений

Пусть и – конечные или бесконечные бинарные нечеткие отношения. Пусть при этом нечеткое отношение задано на декартовом произведении универсумов , а нечеткое отношение – на декартовом произведении универсумов .

Нечеткое бинарное отношение, заданное на декартовом произведении и обозначаемое через , называется Композицией Бинарных нечетких отношений и , а его функция принадлежности определяется выражением

, (3.17)

.

Определенную таким образом композицию бинарных нечетких отношений называют иногда (max-Min)-композицией, или Максиминной Сверткой нечетких отношений.

Можно показать, что эта операция Ассоциативна И Дистрибутивна Относительно нечеткого объединения, но Не дистрибутивна Относительно нечеткого пересечения. Другими словами, для произвольных бинарных нечетких отношений P, Q, R, Заданных на декартовых произведениях , , соответственно, имеют место следующие свойства:

; (3.18)

. (3.19)

Однако

.

Заметим также, что для (max-min)-композиции произвольных бинарных нечетких отношений P, Q, R, заданных на декартовых произведениях , , Соответственно, выполняется следующее свойство Монотонности: Если , то .

Пример 3.15. Фирма для размещения своего филиала приобретает четыре помещения, расположенные на разных этажах в одном здании. Эти помещения предполагается использовать в соответствии с известными целевыми назначениями с учетом их технических характеристик. Построим соответствующую нечеткую модель. С этой целью введем следующие базисные множества.

– набор целевых назначений для использования помещений, где – комната для руководителя; – комната для персонала; – помещение для склада; – помещение для мастерской.

– набор технических характеристик, учитываемых при выборе рационального размещения, где – хорошая естественная освещенность помещения; – большая площадь; – помещение, хорошо отапливаемое; – низкий этаж; – высокий потолок.

– набор приобретаемых помещений.

Введем бинарные нечеткие отношения и , значения функций принадлежности которых представлены в таблицах 3.1 и 3.2.

Таблица 3.1. – Нечеткое отношение , устанавливающее уровень требований к помещениям в соответствии с их предназначением

Тип помещения	Наименование характеристик
Естест. осв.	Больш. площ.	Помещ. хор. отапл.	Низкий этаж	Выс. потолок
Комната для руководителя	0.9	0.4	1.0	0.2	0.6
Комната для персонала	0.8	0.7	1.0	0.1	0.6
Помещение для склада	0.2	0.9	0.2	0.9	0.8
Помещение для мастер.	0.8	0.6	0.6	0.9	0.6

Таблица 3.2. – Нечеткое отношение , устанавливающее степень удовлетворенности предъявляемым требованиям в реальных помещениях

Наименование характеристик	Помещения
Естественная освещенность	0.8	0.9	0.4	0.8
Большая площадь	0.9	0.3	0.9	0.7
Хорошо отапливается	0.2	0.6	0.3	0.9
Низкий этаж	0.8	0.4	0.6	0.3
Высокий потолок	0.7	0.7	0.5	0.6

Соответствующие матрицы нечетких отношений имеют вид

, .

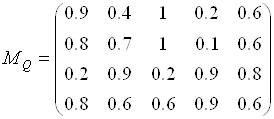В соответствии с (3.17) функция принадлежности композиции бинарных нечетких отношений и определяется выражением

,

.

Результат композиции бинарных отношений и задан матри-

Цей:

.

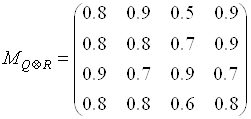В целях наглядности представим полученный результат композиции в виде таблицы 3.3.

Таблица 3.3. – Композиция нечетких отношений и

Тип помещений	Помещения
Комната для руководителя	0.8	0.9	0.5	0.9
Комната для персонала	0.8	0.8	0.7	0.9
Помещение для склада	0.9	0.7	0.9	0.7
Помещение для мастерской	0.8	0.8	0.6	0.8

Рассчитанные на основе композиции бинарных нечетких отношений значения функции принадлежности для всех пар

, I = 1,2,3,4 , K = 1,2,3,4,

Имеют смысл оценки степени целесообразности использования помещения в соответствии с предназначением . Из анализа таблицы 3.3 следует: руководителю разумно предоставить помещение , персоналу – , склад разместить в помещении , а мастерскую в помещении – .

< Предыдущая		Следующая >