12. Основные характеристики нечетких отношений

Пусть – произвольное нечеткое -арное отношение с кортежами из декартова произведения соответствующих универсумов и функцией принадлежности .

Носитель нечеткого отношения. Носителем Нечеткого отношения называется обычное отношение , которое формально определяется следующим образом:

, (3.3)

.

Другими словами, носитель нечеткого отношения содержит те и только те кортежи, для которых значение соответствующей функции принадлежности отлично от 0.

Отношение -уровня. Обобщением понятия нечеткого отношения является Отношение -Уровня, под которым понимается обычное отношение , которое формально определяется следующим образом:

, (3.4)

,

Где – некоторое действительное число, .

Пример 3.10. Отношением -уровня для рассмотренного в примере 3.5 нечеткого отношения может служить отношение: {(<11,11>, 1.0), (<11,12>, 0.8), (<12,11>, 0.8), (<12,12>, 1.0), (<12,13>, 0.8), (<13,12>, 0.8), (<13,13>, 1.0), (<13,14>, 0.8), (<14,13>, 0.8), (<14,14>, 1.0), (<14,15>, 0.8), (<15,14>, 0.8), (<15,15>, 1.0)}.

Высота нечеткого отношения. Высотой нечеткого отношения называется величина , где супремум берется по всем значениям функции принадлежности, соответствующим кортежам .

Например, высота конечного нечеткого отношения равна 1 и соответствует элементам главной диагонали матрицы этого отношения. Высота нечеткого отношения также равна 1, как и для нечеткого отношения из примера 3.9. Однако в этом случае среди элементов универсума отсутствуют кортежи, для которых . Действительно, значение функции принадлежности (3.2) всегда будет строго меньше 1.

Нормальное нечеткое отношение. Нечеткое отношение называется Нормальным, Если максимальное значение его функции принадлежности равно 1. Это означает, что для нормального нечеткого отношения необходимо выполнение условия:

, . (3.5)

Рассмотренные выше нечеткие отношения , , , являются нормальными, поскольку их высота равна 1. Напротив, нечеткое отношение не является нормальным.

Субнормальное нечеткое отношение. Если высота нечеткого отношения равна единице (), но условие (3.5) не выполняется, то такое нечеткое отношение называется Субнормальным.

Очевидно, нечеткое отношение является субнормальным.

Произвольное непустое нечеткое отношение можно сделать субнормальным, используя следующее преобразование:

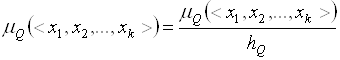. (3.6)

Мода нечеткого отношения. Некоторый кортеж нечеткого отношения называется Модой, Если этот кортеж является точкой локального максимума соответствующей функции принадлежности , то есть выполняется условие:

, (3.7)

Где максимум рассматривается в некоторой локальной окрестности кор-

Тежа из области определения функции принадлежности.

Ядро нечеткого отношения. Ядром Нечеткого отношения называется обычное отношение , которое определяется следующим образом:

, (3.8)

.

Например, ядро нечеткого отношения .

Ближайшее четкое отношение. Ближайшим четким отношением к нечеткому отношению называется четкое отношение, характеристическая функция которого определяется выражением

(3.9)

Например, ближайшее четкое отношение к нечеткому отношению есть отношение: .

Границы, точки перехода, А также свойство выпуклости нечеткого отношения определяются аналогично соответствующим понятиям, введенным для нечетких множеств.

Рассмотрим простейшие отношения между двумя нечеткими отношениями: равенство двух нечетких отношений и нечеткое доминирование.

Равенство нечетких отношений. Два нечетких отношения считаются Равными, Если они заданы на одних и тех же универсумах , имеют одинаковую арность и их функции принадлежности принимают равные значения на всех элементах декартова произведения соответствующих универсумов.

Формально равенство двух нечетких отношений можно записать следующим образом. Произвольное нечеткое отношение равно нечеткому отношению (записывается как ) Тогда и только тогда, когда значения функций принадлежности этих отношений равны для всех элементов декартова произведения их универсумов, то есть выполняется следующее условие:

, (3.10)

.

Нечеткое доминирование. Нечеткое отношение строго включает в себя (строго доминирует) Нечеткое отношение (записывается как ), Если значения функции принадлежности первого строго больше соответствующих значений функции принадлежности второго, т. е. выполняется следующее формальное условие:

, (3.11)

.

Если в этом определении в условии (3.11) вместо знака строгого неравенства записать знак нестрогого неравенства , то получим определение Нестрогого включения Нечетких отношений или Нестрогого доминирования, Которое обозначается как . При этом в случае говорят, что нечеткое отношение доминирует Нечеткое отношение , а нечеткое отношение Содержится В нечетком отношении .

Если для двух нечетких отношений и , Заданных на одних и тех же базисных множествах, не выполняется ни отношение , ни отношение , то эти нечеткие отношения и – Несравнимые.

< Предыдущая		Следующая >