11. Нечеткое отношение и способы его задания
Нечеткое отношение определяется как любое нечеткое подмножество упорядоченных кортежей, построенных из элементов тех или иных базисных множеств – универсумов. При этом под Кортежем, Так же, как и в случае обычных множеств, понимается произвольный набор или список упорядоченных элементов.
Нечеткое отношение. В общем случае Нечетким ![]() -арным отношением, Заданным на множествах (универсумах)
-арным отношением, Заданным на множествах (универсумах) ![]() Называется некоторое нечеткое подмножество декартова произведения этих универсумов. Обозначим произвольное нечеткое отношение через
Называется некоторое нечеткое подмножество декартова произведения этих универсумов. Обозначим произвольное нечеткое отношение через ![]() . По определению,
. По определению, ![]() Где
Где ![]() – функция принадлежности данного нечеткого отношения, которая определяется как отображение
– функция принадлежности данного нечеткого отношения, которая определяется как отображение ![]() Здесь через
Здесь через ![]() обозначен кортеж из
обозначен кортеж из ![]() элементов, каждый из которых выбирается из своего универсу-
элементов, каждый из которых выбирается из своего универсу-
Ма, то есть ![]()
Простейший тип нечетких отношений задается как Бинарное нечеткое отношение между элементами из двух универсальных множеств. При этом на форму и вид функции принадлежности нечеткого отношения предварительно никаких ограничений не накладывается.
Рассмотрим несколько важных частных случаев нечетких отношений.
Пустое нечеткое отношение. В теории нечетких отношений Пустое Нечеткое отношение определяется как отношение, которое не содержит ни одного кортежа. Это отношение обозначается через ![]() и формально определяется как такое нечеткое отношение, функция принадлежности которого тождественно равна 0 на всех элементах декартова произведения его универсумов.
и формально определяется как такое нечеткое отношение, функция принадлежности которого тождественно равна 0 на всех элементах декартова произведения его универсумов.
Полное нечеткое отношение Совпадает с обычным полным отношением, которое, в свою очередь, равно, по определению, декартову произведению соответствующих универсумов ![]() Функция принадлежности полного нечеткого отношения тождественно равна единице для всех без исключения кортежей, т. е.
Функция принадлежности полного нечеткого отношения тождественно равна единице для всех без исключения кортежей, т. е. ![]()
Бинарное нечеткое отношение Задается на базисных множествах ![]() и определяется как нечеткое отношение
и определяется как нечеткое отношение ![]() . Здесь
. Здесь ![]() – функция принадлежности бинарного нечеткого отношения, которая определяется как отображение
– функция принадлежности бинарного нечеткого отношения, которая определяется как отображение ![]() , а через
, а через ![]() обозначен кортеж из двух элементов, причем
обозначен кортеж из двух элементов, причем ![]() .
.
ОбраТное неЧЕТкое отношение. Если задано бинарное нечеткое отношение ![]() на декартовом произведении
на декартовом произведении ![]() , То Обратным К нему нечетким отношением (обозначается через
, То Обратным К нему нечетким отношением (обозначается через ![]() ) называется такое бинарное нечеткое отношение, которое заданно на декартовом произведении
) называется такое бинарное нечеткое отношение, которое заданно на декартовом произведении ![]() , А функция принадлежности которого определяется по следующей формуле:
, А функция принадлежности которого определяется по следующей формуле:
![]() ,
, ![]() ,
, ![]() . (3.1)
. (3.1)
Бинарное нечеткое отношение, заданное на одном базисном множестве (универсуме) ![]() , определяется как нечеткое отношение
, определяется как нечеткое отношение ![]() , где
, где ![]() – функция принадлежности бинарного нечеткого отношения, которая определяется как отображение
– функция принадлежности бинарного нечеткого отношения, которая определяется как отображение ![]() . Здесь через
. Здесь через ![]() обозначен кортеж из двух элементов, причем
обозначен кортеж из двух элементов, причем ![]() .
.
На практике используются различные способы, которыми могут быть формально заданы те или иные нечеткие отношения. Наибольшее распространение из них получили следующие.
В форме Списка с непосредственным перечислением всех кортежей нечеткого отношения и соответствующих этим кортежам значений функции принадлежности: ![]() , где
, где ![]() –
– ![]() -й кортеж
-й кортеж ![]() элементов этого отношения;
элементов этого отношения; ![]() – число кортежей нечеткого отношения
– число кортежей нечеткого отношения ![]() . При этом для сокращения подобной записи кортежи с нулевыми значениями функции принадлежности в списке обычно не указываются. Понятно, что этот способ целесообразно применять только для задания нечетких отношений с конечным и небольшим числом кортежей
. При этом для сокращения подобной записи кортежи с нулевыми значениями функции принадлежности в списке обычно не указываются. Понятно, что этот способ целесообразно применять только для задания нечетких отношений с конечным и небольшим числом кортежей ![]() .
.
Пример 3.1. Отношение задано:
![]() .
.
Аналитически В форме некоторого математического выражения, обеспечивающего возможность вычисления значения функции принадлежности нечеткого отношения для каждого из кортежей. Этот очень удобный способ может быть применен для задания нечетких отношений как с конечным, так и с бесконечным числом кортежей. При его использовании нечеткое отношение записывается в виде:
![]() ,
,
Где ![]() – некоторая заданная функция
– некоторая заданная функция ![]() переменных, удовлетворяющая стандартным требованиям к функциям принадлежности.
переменных, удовлетворяющая стандартным требованиям к функциям принадлежности.
Пример 3.2. Отношение задано аналитически:
![]() .
.
Для задания бинарных отношений, кроме перечисленных, могут дополнительно использоваться и некоторые другие способы.
Графически В форме некоторой поверхности или совокупности отдельных точек в трехмерном пространстве. При этом две координаты (независимые переменные) будут соответствовать значениям элементов ![]() и
и ![]() из универсумов
из универсумов ![]() , а третья координата – функции принадлежности со значениями из интервала [0,1].
, а третья координата – функции принадлежности со значениями из интервала [0,1].
В форме Матрицы Нечеткого отношения. При этом нечеткое бинарное отношение с конечным числом кортежей описывается с использованием матрицы ![]() , первой строке которой соответствуют первые элементы кортежей
, первой строке которой соответствуют первые элементы кортежей ![]() , а первому столбцу – вторые элементы кортежей
, а первому столбцу – вторые элементы кортежей ![]() . Элементами матрицы являются соответствующие значения функции принадлежности
. Элементами матрицы являются соответствующие значения функции принадлежности ![]() Данного отношения. Если бинарное нечеткое отношение задается на одном универсуме, то матрица такого отношения
Данного отношения. Если бинарное нечеткое отношение задается на одном универсуме, то матрица такого отношения ![]() является квадратной.
является квадратной.
Пример 3.3 Отношение задано таблицей: 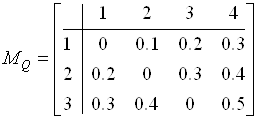 . В тех случаях, когда это не может привести к ошибкам, первую строку и первый столбец опускают. Тогда выделенная из таблицы матрица, задающая приведенное выше отношение, имеет вид
. В тех случаях, когда это не может привести к ошибкам, первую строку и первый столбец опускают. Тогда выделенная из таблицы матрица, задающая приведенное выше отношение, имеет вид 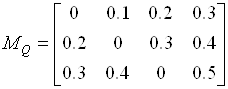 .
.
В форме так называемого ориентированного Нечеткого графа, Который формально может быть задан в виде двух обычных конечных множеств и некоторой функции принадлежности следующим образом: ![]() , где
, где ![]() – множество вершин нечеткого графа,
– множество вершин нечеткого графа, ![]() – множество дуг нечеткого графа, каждой из которых приписано значение функции принадлежности. Натуральное число
– множество дуг нечеткого графа, каждой из которых приписано значение функции принадлежности. Натуральное число ![]() определяет количество вершин конкретного нечеткого графа, а натуральное число
определяет количество вершин конкретного нечеткого графа, а натуральное число ![]() – количество дуг нечеткого графа. При этом дуги с нулевой функцией принадлежности в нечетком графе обычно не изображаются.
– количество дуг нечеткого графа. При этом дуги с нулевой функцией принадлежности в нечетком графе обычно не изображаются.
Каждому ориентированному нечеткому графу ![]() соответствует некоторое бинарное нечеткое отношение
соответствует некоторое бинарное нечеткое отношение ![]() , Состоящее из всех пар вида
, Состоящее из всех пар вида ![]() , где
, где ![]() . При этом для каждой пары
. При этом для каждой пары ![]() определено некоторое действительное число из интервала [0,1], которое равно значению функции принадлежности
определено некоторое действительное число из интервала [0,1], которое равно значению функции принадлежности ![]() для дуги
для дуги ![]() , соединяющей эту пару вершин. При задании нечеткого отношения
, соединяющей эту пару вершин. При задании нечеткого отношения ![]() с помощью ориентированного нечеткого графа
с помощью ориентированного нечеткого графа ![]() каждому элементу универсума
каждому элементу универсума ![]() будет соответствовать отдельная вершина
будет соответствовать отдельная вершина ![]() этого нечеткого графа, а каждому кортежу нечеткого отношения
этого нечеткого графа, а каждому кортежу нечеткого отношения ![]() будет соответствовать дуга графа
будет соответствовать дуга графа ![]() с началом в вершине
с началом в вершине ![]() , концом в вершине
, концом в вершине ![]() и значением функции принадлежности
и значением функции принадлежности ![]() .
.
Пример 3.4. Отношение задано графом
![]()
Рис. 3.1. Ориентированный граф, отображающий бинарное отношение
В зависимости от количества кортежей нечеткое отношение может
Быть конечным или бесконечным. Нечеткое отношение называется Конечным, Если его носитель является конечным отношением. При этом говорят, что такое нечеткое отношение имеет конечную Мощность, Которая численно равна количеству кортежей его носителя, рассматриваемого как обычное множество. В этом случае для обозначения мощности произвольного нечеткого отношения Q Используют общепринятое обозначение Card(Q). Аналогично Счетным Нечетким отношением называется нечеткое отношение со счетным носителем, то есть отношение, носитель которого имеет счетную мощность ![]() . Несчетным Нечетким отношением называется нечеткое отношение с несчетным носителем, то есть носитель которого имеет несчетную мощность или мощность континуума
. Несчетным Нечетким отношением называется нечеткое отношение с несчетным носителем, то есть носитель которого имеет несчетную мощность или мощность континуума ![]() .
.
Пример 3.5. Рассмотрим конечное бинарное нечеткое отношение ![]() , заданное на универсуме
, заданное на универсуме ![]() {11,12,13,14,15} и отображающее свойство: «натуральное число
{11,12,13,14,15} и отображающее свойство: «натуральное число ![]() приблизительно равно натуральному числу
приблизительно равно натуральному числу ![]() ».
».
Соответствующее нечеткое отношение ![]() может быть задано в форме списка следующим образом:
может быть задано в форме списка следующим образом:
![]() {(<11,11>,1.0),(<11,12>,0.8),(<11,13>,0.6), (<11,14>,0.3), (<11,15>,0), (<12,11>,0.8), (<12,12>,1.0), (<12,13>,0.8), (<12,14>,0.6), (<12,15>,0.3), (<13,11>,0.6), (<13,12>,0.8), (<13,13>,1.0), (<13,14>,0.8), (<13,15>,0.6), (<14,11>,0.3), (<14,12>,0.6), (<14,13>,0.8), (<14,14>,1.0), (<14,15>,0.8), (<15,11>,0), (<15,12>,0.3), (<15,13>,0.6), (<15,14>,0.8), (<15,15>,1.0)}.
{(<11,11>,1.0),(<11,12>,0.8),(<11,13>,0.6), (<11,14>,0.3), (<11,15>,0), (<12,11>,0.8), (<12,12>,1.0), (<12,13>,0.8), (<12,14>,0.6), (<12,15>,0.3), (<13,11>,0.6), (<13,12>,0.8), (<13,13>,1.0), (<13,14>,0.8), (<13,15>,0.6), (<14,11>,0.3), (<14,12>,0.6), (<14,13>,0.8), (<14,14>,1.0), (<14,15>,0.8), (<15,11>,0), (<15,12>,0.3), (<15,13>,0.6), (<15,14>,0.8), (<15,15>,1.0)}.
Это же бинарное отношение может быть задано матрицей ![]()
 .
.
Очевидно, что матричное представление нечеткого отношения является гораздо более наглядным, нежели списочное.
Пример 3.6. Рассмотрим теперь другое бинарное нечеткое отношение ![]() , заданное на том же универсуме
, заданное на том же универсуме ![]() {11,12,13,14,15} и отображающее свойство: «натуральное число
{11,12,13,14,15} и отображающее свойство: «натуральное число ![]() несколько больше, чем натуральное число
несколько больше, чем натуральное число ![]() ». Зададим это нечеткое отношение
». Зададим это нечеткое отношение ![]() в матричной форме:
в матричной форме:
 .
.
Пример 3.7. Рассмотрим еще одно бинарное нечеткое отношение ![]() , заданное на том же универсуме
, заданное на том же универсуме ![]() {11,12,13,14,15} и отображающее свойство: «натуральное число
{11,12,13,14,15} и отображающее свойство: «натуральное число ![]() заметно меньше, чем натуральное число
заметно меньше, чем натуральное число ![]() ».
».
Вновь используем матричную форму задания отношения:
 .
.
Пример 3.8. Построим бинарное нечеткое отношение, упрощенно описывающее ситуацию дифференциальной диагностики для группы заболеваний, симптомы проявления которых во многом схожи. В качестве первого универсума рассмотрим совокупность симптомов ![]() , где
, где ![]() – «боль в животе»;
– «боль в животе»; ![]() – «повышение температуры»;
– «повышение температуры»; ![]() – «рвота»;
– «рвота»; ![]() – «снижение диуреза»;
– «снижение диуреза»; ![]() – «увеличение содержания лейкоцитоВ В крови». Второй универсум
– «увеличение содержания лейкоцитоВ В крови». Второй универсум ![]() – набор диагнозов, где
– набор диагнозов, где ![]() – «почечная колика»;
– «почечная колика»; ![]() – «воспаление аппендикса»;
– «воспаление аппендикса»; ![]() – «кишечная инфекция». Здесь между элементами множества диагнозов и множества симптомов существует некоторая причинная связь, но эта связь не однозначна. Поэтому адекватным представлением этой взаимосвязи является бинарное нечеткое отношение
– «кишечная инфекция». Здесь между элементами множества диагнозов и множества симптомов существует некоторая причинная связь, но эта связь не однозначна. Поэтому адекватным представлением этой взаимосвязи является бинарное нечеткое отношение ![]() , заданное на универсумах
, заданное на универсумах ![]() и
и ![]() . При этом значение функции принадлежности
. При этом значение функции принадлежности ![]() отображает степень уверенности в том, что симптом
отображает степень уверенности в том, что симптом ![]() будет проявляться при заболевании
будет проявляться при заболевании ![]() . Зададим это бинарное отношение матрицей
. Зададим это бинарное отношение матрицей ![]() :
:
 .
.
Из анализа этой матрицы следует, что симптом «боль в животе» проявляется при всех перечисленных заболеваниях, симптом «рвота» часто бывает в случае кишечной инфекции, но редко при почечной колике и воспалении аппендикса. А симптом «увеличение содержания лейкоцитов в крови» всегда проявляется при воспалении аппендикса, часто в случае кишечной инфекции, но редко при почечной колике.
Пример 3.9. Рассмотрим бесконечное бинарное нечеткое отношение ![]() , которое задается на одном универсуме
, которое задается на одном универсуме ![]() – множестве неотрицательных действительных чисел
– множестве неотрицательных действительных чисел ![]() . Содержательно отношение
. Содержательно отношение ![]() описывает свойство: "действительное число
описывает свойство: "действительное число ![]() , значительно больше действительного числа
, значительно больше действительного числа ![]() ". Это нечеткое отношение можно задать аналитически, например, с использованием следующей функции принадлежности:
". Это нечеткое отношение можно задать аналитически, например, с использованием следующей функции принадлежности:
![]() , Если
, Если ![]() ,
,
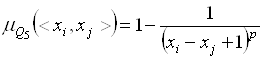 , Если
, Если ![]() ;
; ![]() , целое. (3.2)
, целое. (3.2)
Ясно, что это бесконечное нечеткое отношение нельзя представить в матричной форме или в форме нечеткого графа.
| < Предыдущая | Следующая > |
|---|