10. Нечеткие операторы

Введенные выше нечеткие теоретико-множественные операции не исчерпывают все потенциально возможные способы их задания. В связи с этим большой практический интерес представляет построение обобщенных нечетких параметризованных операторов пересечения, объединения, дополнения и др. Общий и изящный подход к описанию операций пересечения и объединения заключается в их определении в классе Треугольных норм и конорм.

Треугольная норма (Т-норма). Произвольная действительная функция от двух переменных называется Треугольной нормой, если она удовлетворяет следующим свойствам, называемым Аксиомами треугольной нормы:

(ограниченность); (2.36)

(коммутативность); (2.37)

(ассоциативность); (2.38)

, если (монотонность), (2.39)

Приведем примеры треугольных норм.

Операция -Пересечения нечетких множеств:

– операция граничного пересечения:

– операция алгебраического пересечения:

– специальная операция пересечения, задаваемая соотношением:

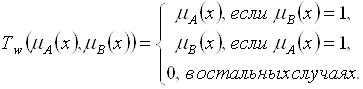
Треугольная конорма (-конорма, -норма). Произвольная действительная функция от двух переменныx называется Треугольной конормой, если она удовлетворяет следующим свойствам, называемым Аксиомами треугольной конормы:

(ограниченность); (2.40)

(коммутативность); (2.41)

(ассоциативность); (2.42)

(монотонность). (2.43)

Приведем примеры треугольных конорм.

Операция -объединения нечетких множеств:

– операция граничного объединения:

– операция алгебраического объединения:

– специальная операция объединения, задаваемая соотношением:

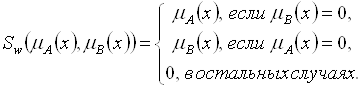
Помимо рассмотренных нечетких операторов треугольной нормы и конормы, обобщающих операции пересечения и объединения, в теории нечетких множеств введены и другие нечеткие операторы, в частности, оператор отрицания, обобщающий операцию дополнения.

Оператор отрицания. Пусть задано некоторое отображение . Это отображение называется Оператором отрицания, если выполняется следующие условия:

(2.44)

Если То. (2.45)

Функция называется Строгим отрицанием, если эта функция непрерывна и она строго убывает.

Функция называется Сильным отрицанием, или Инволюцией, если вместе с условиями (2.44), (2.45) для нее справедливо:

(2.46)

Приведем примеры функции отрицания.

Классическое отрицание (дополнение):

– квадратичное отрицание:

– отрицание Сугено:

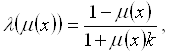
– пороговое дополнение:

Значение , для которого называется равновесной точкой.

Контрольные вопросы

1. Какие простейшие отношения можно определить между нечеткими множествами?

2. Дайте определите основным операциям над нечеткими множествами.

3. Определите функции принадлежности основных операций над нечеткими множествами.

4. В чем состоит разница между унарными и бинарными операциями над нечеткими множествами?

5. Что такое нечеткие операторы? Приведите примеры.

< Предыдущая		Следующая >