09. Бинарные операции над нечеткими множествами
Пусть ![]() и
и ![]() – произвольные (конечные или бесконечные) нечеткие множества, заданные на одном и том же универсуме
– произвольные (конечные или бесконечные) нечеткие множества, заданные на одном и том же универсуме ![]() .
.
Пересечение. Пересечением двух нечетких множеств ![]() и
и ![]() будем называть некоторое третье нечеткое множество
будем называть некоторое третье нечеткое множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , функция принадлежности которого определяется по формуле
, функция принадлежности которого определяется по формуле
![]() ,
, ![]() (2.3)
(2.3)
Операция пересечения нечетких множеств по аналогии с обычными множествами обозначается знаком ![]() . Результат операции пересечения двух нечетких множеств записывается в виде
. Результат операции пересечения двух нечетких множеств записывается в виде ![]() .
.
Понятно, что результат пересечения ![]() Есть наибольшее нечеткое подмножество
Есть наибольшее нечеткое подмножество ![]() , Которое содержится одновременно в нечетких множествах
, Которое содержится одновременно в нечетких множествах ![]() и
и ![]() . Операцию пересечения нечетких множеств в смысле (2.3) иногда называют min-пересечением или
. Операцию пересечения нечетких множеств в смысле (2.3) иногда называют min-пересечением или ![]() -пересечением. Соответствующая функция принадлежности пересечения
-пересечением. Соответствующая функция принадлежности пересечения ![]() записывается в виде
записывается в виде ![]() ,
, ![]() . При этом знак
. При этом знак ![]() используется в качестве синонима операции нахождения минимального значения.
используется в качестве синонима операции нахождения минимального значения.
Операция min-пересечения нечетких множеств корректна в том смысле, что она сохраняет свое определение для случая обычных множеств. Действительно, если в качестве нечетких множеств ![]() и
и ![]() Взять обычные множества как их частный случай, то определение операции пересечения (2.3) превратится в определение операции пересечения для характеристических функций обычных множеств.
Взять обычные множества как их частный случай, то определение операции пересечения (2.3) превратится в определение операции пересечения для характеристических функций обычных множеств.
Пример 2.6. Рассмотрим конечное нечеткое множество ![]() , которое представляет "небольшое натуральное число" И равно:
, которое представляет "небольшое натуральное число" И равно:
![]() .
.
И конечное нечеткое множество ![]() , Которое представляет "натуральное число, приближенно равное двум" И равно:
, Которое представляет "натуральное число, приближенно равное двум" И равно:
![]() .
.
Тогда нечеткое множество ![]() как результат операции пересечения
как результат операции пересечения ![]() будет равно:
будет равно:
![]() .
.
В этом случае нечеткое множество ![]() представляет "небольшое натуральное число, приближенно равное двум".
представляет "небольшое натуральное число, приближенно равное двум".
Результат операции пересечения двух и большего числа нечетких множеств, заданных на одном и том же универсуме ![]() , можно изобразить графически в декартовой системе координат на плоскости.
, можно изобразить графически в декартовой системе координат на плоскости.
Результат операции пересечения двух бесконечных нечетких множеств ![]() и
и ![]() с функциями принадлежностями
с функциями принадлежностями ![]() и
и ![]() приведен на рис. 2.3. При этом каждое из нечетких множеств изображается соответствующей функцией принадлежности, а функция принадлежности результата операции пересечения изображается утолщенной линией.
приведен на рис. 2.3. При этом каждое из нечетких множеств изображается соответствующей функцией принадлежности, а функция принадлежности результата операции пересечения изображается утолщенной линией.
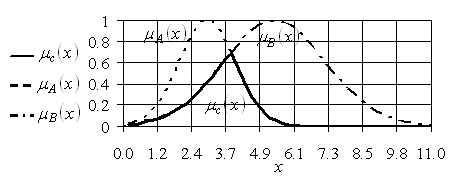
Рис. 2.3. Графическое изображение операции пересечения множеств ![]() и
и ![]()
Отметим следующее свойство выпуклых нечетких множеств. Если нечеткие множества ![]() и
и ![]() – выпуклые, то их пересечение
– выпуклые, то их пересечение ![]() также является выпуклым нечетким множеством.
также является выпуклым нечетким множеством.
Объединение. Объединением двух нечетких множеств ![]() и
и ![]() называется некоторое третье нечеткое множество
называется некоторое третье нечеткое множество ![]() , заданное на том же универсуме
, заданное на том же универсуме ![]() , функция принадлежности которого определяется по формуле
, функция принадлежности которого определяется по формуле
![]() ,
, ![]() . (2.4)
. (2.4)
Операция объединения нечетких множеств по аналогии с обычными множествами обозначается знаком ![]() . Результат операции объединения двух нечетких множеств записывается в виде
. Результат операции объединения двух нечетких множеств записывается в виде ![]() .
.
Понятно, что объединение ![]() есть наименьшее нечеткое множество
есть наименьшее нечеткое множество ![]() , которое доминирует одновременно как
, которое доминирует одновременно как ![]() , так и
, так и ![]() . Операцию объединения нечетких множеств в смысле (2.4) иногда называют mах-объединением или
. Операцию объединения нечетких множеств в смысле (2.4) иногда называют mах-объединением или ![]() -объединением. Соответственно функция принадлежности объединения
-объединением. Соответственно функция принадлежности объединения ![]() в этом случае записывается в виде
в этом случае записывается в виде ![]() ,
, ![]() . При этом знак mах используется в качестве синонима операции нахождения максимального значения.
. При этом знак mах используется в качестве синонима операции нахождения максимального значения.
Операция mах-объединения нечетких множеств также корректна в том смысле, что она сохраняет свое определение для случая обычных множеств. Если в качестве нечетких множеств ![]() и
и ![]() взять обычные множества как их частный случай, то определение операции объединения (2.4) превратится в определение операции объединения для характеристических функций обычных множеств.
взять обычные множества как их частный случай, то определение операции объединения (2.4) превратится в определение операции объединения для характеристических функций обычных множеств.
Пример 2.7. Рассмотрим нечеткое множество ![]() , которое представляет "небольшое натуральное число" и равно:
, которое представляет "небольшое натуральное число" и равно:
![]() {<1,1.0>, <2,1.0>, <3,0.9>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>},
{<1,1.0>, <2,1.0>, <3,0.9>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>},
И нечеткое множество ![]() , которое представляет "натуральное число, приближенно равное трем", и равно:
, которое представляет "натуральное число, приближенно равное трем", и равно:
![]() {<1,0.5>, <2,0.8>, <3,1.0>, <4,0.6>, <5,0.4>, <6,0.1>, <7,0>}.
{<1,0.5>, <2,0.8>, <3,1.0>, <4,0.6>, <5,0.4>, <6,0.1>, <7,0>}.
Тогда нечеткое множество ![]() как результат операции объединения
как результат операции объединения ![]() будет равно:
будет равно:
![]() {<1,1.0>, <2,1.0>, <3,1.0>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>}.
{<1,1.0>, <2,1.0>, <3,1.0>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>}.
В этом случае множество ![]() представляет "небольшое натуральное число или натуральное число, приближенно равное трем".
представляет "небольшое натуральное число или натуральное число, приближенно равное трем".
Результат операции объединения двух и большего числа нечетких множеств, заданных на одном и том же универсуме ![]() , также можно изобразить графически в декартовой системе координат на плоскости.
, также можно изобразить графически в декартовой системе координат на плоскости.
Для случая объединения двух нечетких множеств ![]() , заданных различными функциями принадлежности, результат операции изображен на рис. 2.4.
, заданных различными функциями принадлежности, результат операции изображен на рис. 2.4.
Разность. Разностью двух нечетких множеств ![]() и
и ![]() называется некоторое третье нечеткое множество
называется некоторое третье нечеткое множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , функция принадлежности которого определяется по формуле
, функция принадлежности которого определяется по формуле
![]() . (2.5)
. (2.5)
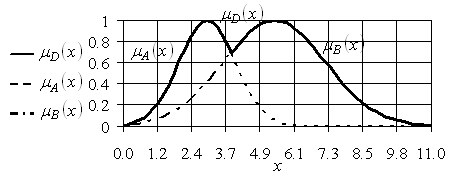
Рис. 2.4. Графическое изображение операции объединения множеств ![]() и
и ![]()
Операция разности двух нечетких множеств по аналогии с обычными множествами обозначается знаком ![]() . Результат операции разности двух нечетких множеств записывается в виде
. Результат операции разности двух нечетких множеств записывается в виде ![]() .
.
Пример 2.8. Рассмотрим нечеткое множество
![]() {<1,1.0>, <2,1.0>, <3,0.9>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>},
{<1,1.0>, <2,1.0>, <3,0.9>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>},
Представляющее "небольшое натуральное число", и нечеткое множество ![]() , которое представляет "натуральное число, приближенно равное трем", и равно:
, которое представляет "натуральное число, приближенно равное трем", и равно:
![]() {<1,0.5>, <2,0.8>, <3,1.0>, <4,0.6>, <5,0.4>, <6,0.1>, <7,0>}.
{<1,0.5>, <2,0.8>, <3,1.0>, <4,0.6>, <5,0.4>, <6,0.1>, <7,0>}.
Тогда нечеткое множество ![]() как результат операции разности
как результат операции разности ![]() будет равно:
будет равно:
![]() {<1,0.5>,<2,0.2>, <3,0>, <4,0.2>, <5.0.1>, <6,0.1>, <7,0.1>}.
{<1,0.5>,<2,0.2>, <3,0>, <4,0.2>, <5.0.1>, <6,0.1>, <7,0.1>}.
В этом случае нечеткое множество ![]() представляет "небольшое натуральное число, не являющееся приближенно равным трем".
представляет "небольшое натуральное число, не являющееся приближенно равным трем".
Результат выполнения операции разности двух нечетких множеств ![]() и
и ![]() , заданных на одном и том же универсуме
, заданных на одном и том же универсуме ![]() различными функциями принадлежности, изображен на рис. 2.5.
различными функциями принадлежности, изображен на рис. 2.5.
Симметрическая разность. Операция разности двух нечетких множеств в отличие от операций ![]() -объединения и
-объединения и ![]() -пересечения не является коммутативной, т. е. в общем случае
-пересечения не является коммутативной, т. е. в общем случае ![]() . Вместе с тем при решении многих практических задач оказывается полезной коммутативная операция Симметрической разности Двух нечетких множеств
. Вместе с тем при решении многих практических задач оказывается полезной коммутативная операция Симметрической разности Двух нечетких множеств ![]() и
и ![]() (обозначим ее через
(обозначим ее через ![]() ). Результатом выполнения этой операции для двух нечетких множеств
). Результатом выполнения этой операции для двух нечетких множеств ![]() и
и ![]() является некоторое третье нечеткое множество
является некоторое третье нечеткое множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , функция принадлежности которого определяется по формуле:
, функция принадлежности которого определяется по формуле:
![]() . (2.6)
. (2.6)
Легко проверить, что ![]() , то есть симметрическая разность двух нечетких множеств представляет собой объединение двух разностей нечетких множеств
, то есть симметрическая разность двух нечетких множеств представляет собой объединение двух разностей нечетких множеств ![]() и
и ![]() .
.
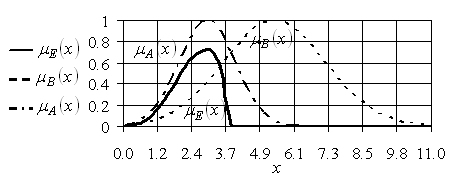
Рис. 2.5. Графическое изображение операции разности нечетких множеств ![]() и
и ![]()
Определенные выше операции разности и симметрической разности двух нечетких множеств корректны в том смысле, что они остаются справедливыми для случая обычных множеств.
Пример 2.9. Вновь рассмотрим нечеткое множество
![]() {<1,1.0>, <2,1.0>, <3,0.9>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>},
{<1,1.0>, <2,1.0>, <3,0.9>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>},
Представляющее "небольшое натуральное число", и нечеткое множество ![]() , которое представляет "натуральное число, приближенно равное трем", и равно:
, которое представляет "натуральное число, приближенно равное трем", и равно:
![]() {<1,0.5>, <2,0.8>, <3,1.0>, <4,0.6>, <5,0.4>, <6,0.1>, <7,0>}.
{<1,0.5>, <2,0.8>, <3,1.0>, <4,0.6>, <5,0.4>, <6,0.1>, <7,0>}.
Их симметрическая разность ![]() будет равна:
будет равна:
![]() ={<1,0.5>, <2,0.2>, <3,0.1>, <4,0.2>, <5,0.1>, <6,0.1>, <7,0.1>}.
={<1,0.5>, <2,0.2>, <3,0.1>, <4,0.2>, <5,0.1>, <6,0.1>, <7,0.1>}.
Результат выполнения операции симметрической разности двух
Нечетких множеств ![]() и
и ![]() , заданных на одном и том же универсуме
, заданных на одном и том же универсуме ![]() , изображен на рис. 2.6.
, изображен на рис. 2.6.
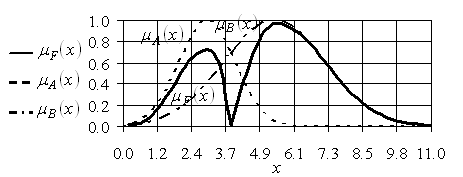
Рис. 2.6. Графическое изображение операции симметрической разности нечетких множеств ![]() и
и ![]()
Рассмотренные операции над нечеткими множествами обладают следующими фундаментальными свойствами, аналогичными свойствам обычных теоретико-множественных операций.
Пусть ![]() и
и ![]() – произвольные (конечные или бесконечные) нечеткие множества, заданные на одном и том же универсуме
– произвольные (конечные или бесконечные) нечеткие множества, заданные на одном и том же универсуме ![]() . Справедливы следующие утверждения.
. Справедливы следующие утверждения.
Коммутативность операций объединения и пересечения нечетких множеств:
![]() ;
; ![]() . (2.7)
. (2.7)
Ассоциативность Операций объединения и пересечения нечетких множеств:
![]() ;
; ![]() . (2.8)
. (2.8)
Дистрибутивность Операций объединения и пересечения нечетких множеств относительно друг друга:
![]() ;
;
![]() . (2.9)
. (2.9)
Идемпотентность Операций объединения и пересечения нечетких множеств:
![]() ;
; ![]() . (2.10)
. (2.10)
Поглощение Одного из нечетких множеств при операциях объединения и пересечения:
![]() . (2.11)
. (2.11)
Универсальные верхняя и нижняя границы (единичные элементы) операций пересечения и объединения нечетких множеств:
![]() ;
;![]() ; (2.12)
; (2.12)
![]() ,
, ![]() . (2.13)
. (2.13)
Инволюция (двойное дополнение) нечеткого множества:
![]() . (2.14)
. (2.14)
Законы Де Моргана:
![]() ;
; ![]() . (2.15)
. (2.15)
Вместе с тем следует заметить, что для рассматриваемых операции над нечеткими множествами Не Выполняются закон Исключенного третьего И закон Тождества (свойства дополняемости операций пересечения и объединения). А именно в общем случае оказываются справедливыми неравенства:
![]() ; (2.16)
; (2.16)
![]() . (2.17)
. (2.17)
Кроме того, отметим, что для операций min-пересечения и max-объединения нечетких множеств возможны и другие альтернативные способы их определения, корректные в смысле соответствия обычным теоретико-множественным операциям.
Пусть ![]() и
и ![]() – произвольные (конечные или бесконечные) нечеткие множества, заданные на одном и том же универсуме
– произвольные (конечные или бесконечные) нечеткие множества, заданные на одном и том же универсуме ![]() .
.
Алгебраическое пересечение. Алгебраическим пересечением (или Алгебраическим произведением) Двух нечетких множеств ![]() и
и ![]() называется некоторое третье нечеткое множество
называется некоторое третье нечеткое множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , Функция принадлежности которого определяется по формуле
, Функция принадлежности которого определяется по формуле
![]() . (2.18)
. (2.18)
Алгебраическое пересечение двух нечетких множеств ![]() и
и ![]() обозначается через
обозначается через ![]() .
.
Пример 2.10. Вернемся к введенным выше нечеткому множеству
![]() {<1,1.0>, <2,1.0>, <3,0.9>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>},
{<1,1.0>, <2,1.0>, <3,0.9>, <4,0.8>, <5,0.5>, <6,0.2>, <7,0.1>},
И нечеткому множеству
![]() {<1,0.5>, <2,0.8>, <3,1.0>, <4,0.6>, <5,0.4>, <6,0.1>, <7,0>}.
{<1,0.5>, <2,0.8>, <3,1.0>, <4,0.6>, <5,0.4>, <6,0.1>, <7,0>}.
Тогда нечеткое множество ![]() , Являющееся результатом операции алгебраического пересечения
, Являющееся результатом операции алгебраического пересечения ![]() , будет равно:
, будет равно:
![]() {<1,0.5>,<2,0.8>,<3,0.9>,<4,0.48>,<5,0.2>,<6,0.02>,<7,0>}.
{<1,0.5>,<2,0.8>,<3,0.9>,<4,0.48>,<5,0.2>,<6,0.02>,<7,0>}.
Результат операции алгебраического пересечения двух бесконечных нечетких множеств ![]() и
и ![]() , заданных различными функциями принадлежности, иллюстрируется на рис. 2.7.
, заданных различными функциями принадлежности, иллюстрируется на рис. 2.7.
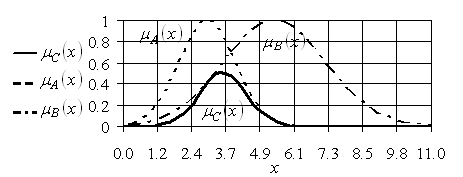
Рис. 2.7. Графическое изображение операции алгебраического пересечения нечетких множеств ![]() и
и ![]()
Алгебраическое объединение. Алгебраическим объединением (или Алгебраическим суммой) Двух нечетких множеств ![]() и
и ![]() называется нечеткое множество
называется нечеткое множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , функция принадлежности которого определяется по формуле
, функция принадлежности которого определяется по формуле
![]() . (2.19)
. (2.19)
Алгебраическое объединение двух нечетких множеств ![]() и
и ![]() обозначается через
обозначается через ![]() .
.
Пример 2.11. Для этих же нечетких множеств ![]() и
и ![]() (пример 2.10) результат алгебраического объединения будет равен:
(пример 2.10) результат алгебраического объединения будет равен:
![]() {<1,1>, <2,1>, <3,1>, <4,0.92>, <5,0.7>, <6,0.28>, <7,0.1>}.
{<1,1>, <2,1>, <3,1>, <4,0.92>, <5,0.7>, <6,0.28>, <7,0.1>}.
Графическая иллюстрация операции алгебраического объединения двух бесконечных нечетких множеств, заданных на одном и том же универсуме ![]() , представлена на рис. 2.8.
, представлена на рис. 2.8.
Операции алгебраического пересечения и алгебраического объединения нечетких множеств обладают лишь некоторыми из свойств, аналогичных свойствам обычных теоретико-множественных операций. При этом справедливы следующие утверждения.
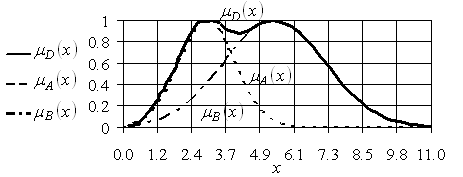
Рис. 2.8. Графическое изображение операции алгебраического объединения нечетких множеств ![]() и
и ![]()
Коммутативность Операций алгебраического объединения и пересечения нечетких множеств:
![]() ;
; ![]() . (2.20)
. (2.20)
Ассоциативность Операций алгебраического объединения и пересечения нечетких множеств:
![]() ;
; ![]() . (2.21)
. (2.21)
Универсальные верхняя и нижняя границы (единичные элементы) операций алгебраического пересечения и объединения нечетких множеств:
![]()
![]() (2.22)
(2.22)
![]() ,
,![]() (2.23)
(2.23)
Законы де Моргана:
![]()
![]() (2.24)
(2.24)
Однако в общем случае остальные свойства Не выполняются. Справедливы следующие утверждения.
Недистрибутивность операций алгебраического объединения и пересечения нечетких множеств относительно друг друга:
![]()
![]() (2.25)
(2.25)
Неидемпотентность операций алгебраического объединения и пересечения нечетких множеств:
![]()
![]() (2.26)
(2.26)
Непоглощение Одного из нечетких множеств при операциях алгебраического объединения и пересечения:
![]()
![]() (2.27)
(2.27)
Не выполняются закон Исключенного третьего и закон противоречия:
![]() (2.28)
(2.28)
![]() (2.29)
(2.29)
Продолжим рассмотрение операций над нечеткими множествами.
Граничное пересечение. Граничным пересечением двух нечетких множеств ![]() и
и ![]() называется нечеткое множество
называется нечеткое множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , функция принадлежности которого определяется по формуле:
, функция принадлежности которого определяется по формуле:
![]()
![]() (2.30)
(2.30)
Граничное пересечение нечетких множеств обозначается ![]()
Пример 2.12. Для приведенных выше нечетких множеств ![]() и
и ![]() результат граничного пересечения нечетких множеств
результат граничного пересечения нечетких множеств ![]() и
и ![]() будет равен:
будет равен:
![]() .
.
Результат операции граничного пересечения двух бесконечных нечетких множеств ![]() и
и ![]() , заданных различными функциями принадлежности, изображен рис. 2.9.
, заданных различными функциями принадлежности, изображен рис. 2.9.

Рис. 2.9. Графическое изображение операции граничного пересечения нечетких множеств ![]() и
и ![]()
Граничное объединение. Граничным объединением двух нечетких множеств ![]() и
и ![]() называется нечеткое множество
называется нечеткое множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , функция принадлежности которого определяется по следующей формуле:
, функция принадлежности которого определяется по следующей формуле:
![]() ,
,![]() . (2.31)
. (2.31)
Граничное объединение двух нечетких множеств ![]() и
и ![]() обозначается через
обозначается через ![]() .
.
Пример 2.13. Результат операции граничного объединения для приведенных выше нечетких множеств ![]() и
и ![]() равен:
равен:
![]() .
.
Графическая иллюстрация операции граничного объединения двух бесконечных нечетких множеств ![]() и
и ![]() , заданных различными функциями принадлежности, изображена рис. 2.10.
, заданных различными функциями принадлежности, изображена рис. 2.10.
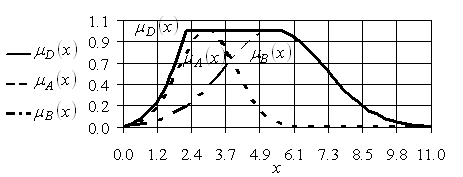
Рис. 2.10. Графическое изображение операции граничного объединения нечетких множеств ![]() и
и ![]()
Операция ![]() -Суммы нечетких множеств.
-Суммы нечетких множеств. ![]() -Суммой двух нечетких множеств
-Суммой двух нечетких множеств ![]() и
и ![]() называется множество
называется множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , функция принадлежности которого определяется по формуле
, функция принадлежности которого определяется по формуле
![]()
![]() (2.32)
(2.32)
Где параметр ![]() .
.
Эта операция обозначается через ![]() .
.
Для введенных альтернативных операций над нечеткими множествами справедливо следующее соотношение:
![]() . (2.33)
. (2.33)
Эти неравенства означают, что для произвольных нечетких множеств ![]() и
и ![]() результат более левой операции всегда будет являться нечетким подмножеством результата более правой операции.
результат более левой операции всегда будет являться нечетким подмножеством результата более правой операции.
Обобщением операции ![]() -Суммы Двух нечетких множеств является операция определения выпуклой комбинации произвольного конечного числа нечетких множеств. Пусть
-Суммы Двух нечетких множеств является операция определения выпуклой комбинации произвольного конечного числа нечетких множеств. Пусть ![]() – нечеткие множества, заданные на универсуме
– нечеткие множества, заданные на универсуме ![]() , а
, а ![]() – неотрицательные действительные числа, сумма которых равна 1.
– неотрицательные действительные числа, сумма которых равна 1.
Выпуклая комбинация нечетких множеств. Выпуклой комбинацией нечетких множеств ![]() называется нечеткое множество
называется нечеткое множество ![]() , функция принадлежности которого определяется по формуле
, функция принадлежности которого определяется по формуле
![]()
![]() (2.34)
(2.34)
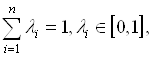
![]()
Дизъюнктивная сумма. Дизъюнктивной суммой двух нечетких множеств ![]() и
и ![]() называется некоторое третье множество
называется некоторое третье множество ![]() , заданное на этом же универсуме
, заданное на этом же универсуме ![]() , функция принадлежности которого определяется по формуле
, функция принадлежности которого определяется по формуле
![]()
![]() (2.35)
(2.35)
Эквивалентная запись для определения операции дизъюнктивной суммы имеет вид ![]() .
.
Пример 2.14. Для введенного ранее нечеткого множества:
![]()
И нечеткого множества
![]() ,
,
Результат их дизъюнктивной суммы будет равен: ![]()
![]() .
.
| < Предыдущая | Следующая > |
|---|