08. Унарные операции над нечеткими множествами

Рассмотрим основные унарные операции, которые используются при построении нечетких моделей сложных систем.

Дополнение. Дополнением нечеткого множества называется нечеткое множество , заданное на том же универсуме , функция при-

Надлежности которого определяется по формуле:

, . (2.1)

Пример 2.2. Рассмотрим конечное нечеткое множество , которое представляет «небольшое натуральное число» и равно

И нечеткое множество , представляющее «натуральное число, приближенно равное трем» и равное

Их дополнения будут равны:

При этом нечеткое множество представляет "натуральное число, не являющееся небольшим", А нечеткое множество – "натуральное число, не равное приближенно трем".

Операция дополнения для бесконечного нечеткого множества представлена графически на рис. 2.1.

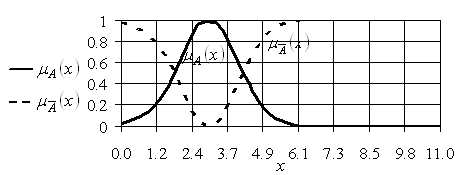
Рис. 2.1. Графическое изображение операции дополнения нечеткого множества

Для конечных нечетких множеств операция дополнения может быть использована с целью расчета показателя размытости по формуле

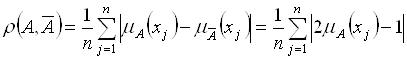Если при этом для расчета вместо хэмминговой метрики использовать колмогорову, то эта формула примет вид

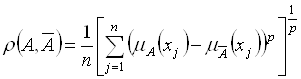, – положительное, целое число.

Возведение в степень. Пусть – произвольное нечеткое множество, заданное на универсуме , – положительное действительное число Операцию Возведения в степень Определим по формуле

, . (2.2)

Эту операцию обычно обозначают через .

Пример 2.3. Для конечного нечеткого множества:

И числа нечеткое множество равно:

Операция возведения бесконечного нечеткого множества с гауссовой функцией принадлежности (1.27) для , в степень иллюстрируется графически на рис. 2.2.

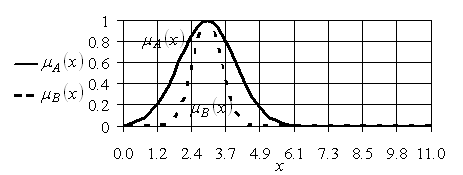
Рис. 2.2. Графическое изображение операции возведения в степень нечеткого множества

Операция возведения в степень используется для осуществления специальных преобразований функций принадлежности нечетких множеств: концентрирования и растяжения.

Концентрирование. Пусть на универсуме задано произвольное нечеткое множество с функцией принадлежности . Операция Концентрирования, Обозначаемая через , дает в результате нечеткое множество , функция принадлежности которого равна значениям функции принадлежности исходного нечеткого множества, возведенным в степень , то есть

, .

Пример 2.4. Для конечного нечеткого множества и его концентрирование равно:

Растяжение. Операция Растяжения, Обозначаемая через , дает в результате нечеткое множество , функция принадлежности которого равна значениям функции принадлежности исходного нечеткого множества, возведенным в степень , то есть

, .

Пример 2.5. Для конечного нечеткого множества и его растяжение равно:

Применение операции концентрирования к нечеткому множеству приводит к уменьшению нечеткости или неопределенности в задании этого множества. Напротив, в результате применения операции растяжения происходит усиление неопределенности в задании нечеткого множества.

< Предыдущая		Следующая >