03. Основные характеристики нечетких множеств

Пусть – произвольное нечеткое множество (конечное или бесконечное) с элементами из универсума и функцией принадлежности .

Множеством Уровня (-срезом) нечеткого множества называется нечеткое подмножество универсального множества , определяемое по формуле

, где .

Множество строгого уровня определяется в виде . В частности, носителем нечеткого множества является множество строго уровня множества , то есть множество элементов, для которых .

Пример 1.4. Рассмотрим нечеткое множество, представляющее "небольшое натуральное число" и равное:

Тогда некоторые из его множеств -уровня: , , .

В случае бесконечных нечетких множеств для построения множеств -уровня следует на графике соответствующей функции принадлежности провести прямую линию . После этого нужно на оси выделить те точки или интервалы, для которых соответствующие части графика расположены не ниже этой линии.

Пример 1.5. Рассмотрим бесконечное нечеткое множество , ко-

Торое представляет "действительное число, приближенно равное нулю", с функцией принадлежности

График этой функции приведен на рис. 1.3. Описанным выше способом получим, например, множество 0.5-уровня (рис. 1.4). При этом .

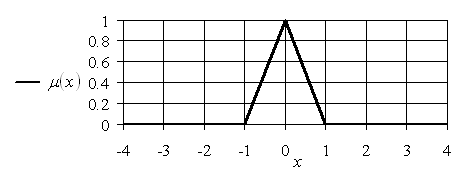
Рис. 1.3. Графическое изображение функции принадлежности бесконечного нечеткого множества «действительное число, приближенно равное нулю»

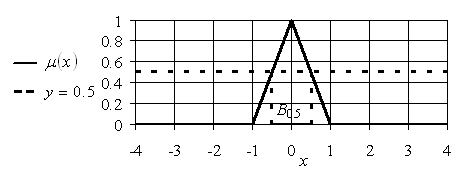
Рис. 1.4. Графическое изображение функции принадлежности бесконечного нечеткого множества 0.5-уровня «действительное число, приближенно равное нулю»

Заметим, что для всех множеств -уровня произвольного нечеткого множества справедливо следующее утверждение: если , то .

Высота нечеткого множества. Величина , где су-

Премум берется по всем значениям , называется Высотой Нечеткого множества .

При этом высота конечного нечеткого множества "небольшое натуральное число" из примера 1.4 равна 1 и соответствует двум элементам универсума: 1 и 2. Высота нечеткого множества , которое представляет "действительное число, приближенно равное нулю" в примере 1.5, также равна 1 и .

Пример 1.6. Рассмотрим бесконечное нечеткое множество , которое представляет "большое действительное число" с функцией принадлежности, заданной следующим математическим выражением:

, .

Высота этого нечеткого множества также равна 1, среди элементов универсума отсутствуют числа, для которых (рис. 1.5).

Нормальное нечеткое множество. Нечеткое множество называется Нормальным, если

. (1.10)

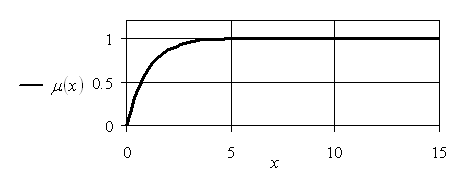
Рис. 1.5. Графическое изображение функции принадлежности нечеткого множества «большое действительное число»

Субнормальное нечеткое множество. Нечеткое множество называется Субнормальным, если его высота равна 1, но условие (1.10) не выполняется.

Произвольное непустое нечеткое множество можно привести к нормальному (то есть нормализовать) по формуле

.

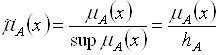Пример 1.7. Нечеткое множество "небольшое натуральное число" (пример 1.4) является нормальным, поскольку его высота равна 1 и соответствует двум его элементам: 1 и 2. Нечеткое множество "действительное число, приближенно равное нулю" также является нормальным, поскольку его высота равна 1 и

Однако нечеткое множество «большое действительное число» является субнормальным, так как условие (1.10) не выполняется ни для какого, но , .

Унимодальное нечеткое множество. Нечеткое множество называется унимодальным, если его функция принадлежности является унимодальной на носителе множества .

При этом точка является точкой максимума функции принадлежности, если

, (1.11)

Где – -окрестность точки .

Любая точка нечеткого множества , удовлетворяющая условию (1.11), называется Модальным значением или Модой нечеткого множества .

Если точка , удовлетворяющая (1.11), является единственной, то соответствующая функция принадлежности называется Строго унимодальной.

Ядро нечеткого множества. Ядром Нечеткого множества называется четкое множество , элементы которого удовлетворяют условию:

. (1.12)

Например, ядро нечеткого множества "небольшое натуральное число" Равно двухэлементному множеству . Ядро нечеткого множества "действительное число, приближенно равное нулю" равно одноэлементному множеству . Нечеткое множество "большое действительное число" имеет пустое ядро.

Понятно, что если произвольное нечеткое множество является субнормальным, то ядро такого нечеткого множества будет пустым.

Границы нечеткого множества. Границами нечеткого множеств называются такие элементы универсума, для которых значения функции принадлежности отличны от 0 и 1. Другими словами, границы нечеткого множеств включают те и только те элементы универсума , для которых выполняется условие: .

Точки перехода нечеткого множества. Элементы нечеткого множества , для которых выполняется условие: , называются Точками перехода этого нечеткого множества .

Ближайшее четкое множество. Четкое множество, Ближайшее К нечеткому множеству , определяется следующим выражением:

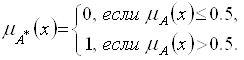(1.13)

Выпуклое нечеткое множество. Нечеткое множество с универсумом называют Выпуклым, если для каждой пары точек , его функция принадлежности удовлетворяет неравенству

, .

На рис. 1.6 и 1.7 изображены графики двух функций принадлежности, первая из которых является выпуклой, а вторая – не является выпуклой.

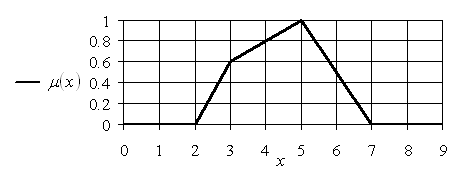
Рис. 1.6. График функции принадлежности выпуклого нечеткого множества

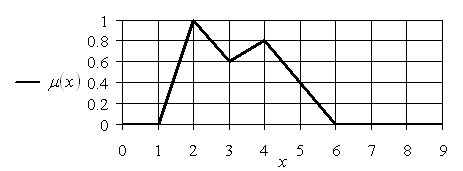
Рис. 1.7. График функции принадлежности невыпуклого нечеткого множества

Кроме того, следует заметить, что первая функция принадлежности является строго унимодальной с модой , а вторая – не является унимодальной и имеет два модальных значения: и .

Показатель размытости нечетких множеств. Уже отмечалось, что нечеткие множества используются для описания плохо определенных объектов, понятий, неоднозначно понимаемых и трактуемых ситуаций. Де Лука предложил ввести показатель этой неопределенности, который назван Показателем размытости (или мерой энтропии) нечетких множеств. В качестве этого показателя предложен функционал, аналогичный шенноновской энтропии, используемой в теории информации. Представляется достаточно очевидной возможность различной трактовки показателя размытости нечетких множеств. Во-первых, это числовая характеристика внутренней неопределенности, двусмысленности, противоречивости, обусловленной неполной (частичной) принадлежностью объектов рассматриваемому множеству. Во-вторых, показатель размытости – мера отличия нечеткого множества от ближайшего четкого множества. Понятно, что технология расчета показателя размытости зависит от того, какая именно трактовка этого показателя выбрана для оценки рассматриваемого нечеткого множества.

Показатель размытости как мера внутренней неопределенности, двусмысленности объектов множества по отношению к некоторому конкретному свойству, характеризующему эти объекты и определяющему в некоторое множество объектов , рассчитывается следующим образом. Если какой-либо объект обладает упомянутым конкретным свойством, но лишь частично, то меру принадлежности рассматриваемого объекта к множеству объектов, обладающих этим свойством, можно оценить значением функции принадлежности . Внутренняя неопределенность, двусмысленность объекта по отношению к этому свойству проявляется в том, что объект, хотя и в разной степени, принадлежит двум противоположным классам: классу объектов, Обладающих выбранным свойством, и классу объектов, Не обладающих этим свойством. Эта двусмысленность максимальна, когда степени принадлежности объекта к обоим классам равны, то есть . И наоборот, двусмысленность минимальна, когда объект определенно принадлежит одному из классов, то есть , , либо , .

Один из возможных способов расчета показателя размытости для конечного множества , содержащего элементов, состоит в вычислении шенноновской логарифмической энтропии нечеткого множества

,

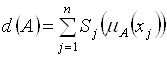Где

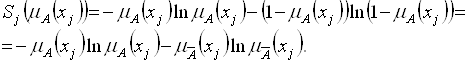
С другой стороны, показатель размытости может быть определен с помощью метрики как мера отличия нечеткого множества от ближайшего к нему обычного множества.

Как уже отмечалось, множеством , ближайшим к нечеткому множеству , является четкое, неразмытое множество с характеристической функцией

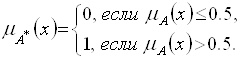
Тогда показатель размытости определяется соотношением

.

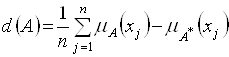Если в последнем соотношении вместо хэмминговой метрики использовать колмогоровскую, то формула для расчета показателя размытости примет вид:

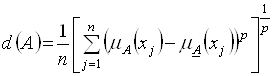, – положительное, целое число.

Ясно, что в частных случаях, когда , получим хэммингово расстояние, а при – евклидово.

< Предыдущая		Следующая >