02. Основные определения теории нечётких множеств

Одно из фундаментальных направлений классической математики – теория множеств, введенная Г. Кантором, не только реформировала основные концепции и язык математики, но и привела к постановке и решению многих теоретических и практических задач, которые ранее вообще не могли рассматриваться как объекты применения математических методов. Теория множеств оперирует с множествами и элементами, из которых они составлены. Интуитивно ясное определение множества принадлежит основателю теории Г. Кантору: «Множество есть объединение в одно целое объектов, обладающих некоторыми общими свойствами».

Основные понятия теории множеств формально вводятся следующим образом.

Пусть есть множество, – подмножество . Этот факт формально отображается следующим образом:

.

Если элемент множества есть элемент подмножества , то этот факт обозначается формулой

.

Множество есть Универсальное множество (универсум), если из его элементов формируются все подмножества, рассматриваемые в выбранном классе задач. Примеры универсальных множеств: множество вещественных чисел, множество чисел натурального ряда, множество непрерывных функций, множество дней недели, множество жителей ре-

Гиона и т. д.

Для выражения принадлежности элемента подмножеству используют понятие Характеристической функции , значение которой указывает, является ли элементом :

Пример. Пусть

,

.

Запишем теперь для каждого элемента из степень его принадлежности подмножеству . Имеем:

, , , , , .

На практике используются и другие, эквивалентные способы описания степени принадлежности элементов из подмножеству :

,

Или

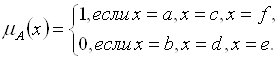
Относительно подмножеств универсального множества введены следующие операции.

Для двух любых подмножеств и Пересечением называется подмножество такое, что , если и одновременно , то есть

. (1.1)

Операция пересечения может быть введена иначе:

. (1.2)

Для двух любых подмножеств и Объединением называется множество такое, что , если , но , или , но , или наконец и , то есть

. (1.3)

Используется и другая форма задания значения характеристической функции результата объединения:

. (1.4)

В приведенных соотношениях операции и определяются таблицами на рис. 1.1 и 1.2.

0
Рис. 1.1. Определение операции	Рис. 1.2. Определение операции

Дополнением относительно называется такое подмножество , для которого

, (1.5)

При этом если

, то ,

То есть, если

, то .

Теория нечетких множеств представляет собой обобщение и, в известной мере, переосмысление основных понятий и формализмов обычной теории множеств. У ее истоков лежат идеи многозначной логики, определившей возможность перехода от двух к произвольному числу значений истинности; теории вероятностей, которая, породив возможность корректного описания неопределенности экспериментальных данных, открыла пути определения и интерпретации не обязательно булевой функции принадлежности; дискретной математики, предложившей инструмент построения моделей многоуровневых систем и, наконец, собственно теории множеств, формальный аппарат которой послужил основанием для появления и развития нечеткой теории множеств.

Нечеткое множество Представляет собой совокупность элементов произвольной природы, относительно каждого из которых нельзя с полной определенностью утверждать – принадлежит ли этот элемент рассматриваемой совокупности данному множеству или нет. Другими словами, нечеткое множество отличается от обычного множества тем, что для всех или части его элементов не существует однозначного ответа на вопрос: "Принадлежит или не принадлежит тот или иной элемент рассматриваемому нечеткому множеству?"

Подход к формализации понятия нечеткого множества состоит в обобщении понятия характеристической функции. При этом Нечеткие множества есть естественное обобщение обычных множеств на случай, когда характеристические функции могут принимать не только значения или , но любое значение в интервале . В теории нечетких множеств характеристическая функция называется Функцией принадлежности, а ее значение – степенью принадлежности элемента нечеткому множеству .

Формально нечеткое множество Определяется как множество упорядоченных пар, или кортежей вида: , где является элементом некоторого универсального множества или универсума , a – Функция принадлежности, Которая ставит в соответствие каждому из элементов некоторое действительное число из интервала , то есть эта функция определяется в форме отображения:

. (1.6)

При этом значение для некоторого означает, что элемент ОпредеЛенно принадлежит Нечеткому множеству , а значение означает, что элемент определенно не принадлежит Нечеткому множеству .

Формально нечеткое множество, содержащее конечное число элементов, принято записывать следующим образом: , а в общем случае – в виде: .

Пример 1.1. Пусть

,

.

Тогда будем говорить, что элемент не принадлежит множеству , элемент принадлежит ему в малой степени, элемент более или менее принадлежит, элемент принадлежит в значительной степени,

Элемент является элементом множества .

Пример 1.2. Пусть – множество чисел натурального ряда:

.

Тогда нечеткое множество «небольших неотрицательных целых чисел» может быть введено следующим образом:

.

Заметим, что в литературе по нечетким множествам иногда используются другие обозначения для описания нечетких множеств.

Так, нечеткое множество из примера 1.2 может быть записано следующим образом:

Или

.

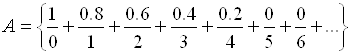Здесь вертикальная или горизонтальная черточки – просто разделители, а знак «+» обозначает не арифметическую операцию сложения, а теоретико-множественное объединение отдельных элементов.

Из всех нечетких множеств выделим два частных случая, имеющих свои классические аналоги. Таким является Пустое нечеткое множество, которое не содержит ни одного элемента. Оно обозначается символом и формально определяется как такое нечеткое множество, функция принадлежности элементов которого тождественно равна нулю для всех без исключения элементов: , .

Другое специальное множество – универсум уже было введено выше в качестве обычного множества, содержащего в выбранном классе задач все возможные элементы. Формально следует считать, что функция принадлежности элементов универсума как нечеткого множества тождественно равна единице для всех без исключения его элементов: , .

Введем теперь понятие носителя нечеткого множества.

Носителем Нечеткого множества называется обычное множест-

Во , Которое содержит те и только те элементы универсума, для которых значения функции принадлежности соответствующего нечеткого множества отличны от нуля. Математически носитель нечеткого множества определяется следующим образом:

. (1.7)

Заметим, что во многих работах для описания носителя используется обозначение Supp (от англ. Support).

Понятно, что пустое нечеткое множество имеет пустой носитель, а носитель универсума, рассматриваемого как нечеткое множество, совпадает с самим универсумом. Заметим, что для записи произвольного нечеткого множества обычно указывают значения его функции принадлежности для элементов носителя, поскольку значения функции принадлежности для всех остальных элементов равны нулю.

В зависимости от количества элементов в нечетком множестве, по аналогии с обычными множествами, можно определить конечные и бесконечные нечеткие множества.

Нечеткое множество называется Конечным, если его носитель является конечным множеством. При этом говорят, что такое нечеткое множество имеет конечную мощность, которая численно равна количеству элементов его носителя как обычного множества. Для задания мощности произвольного нечеткого множества используется обозначение . Естественно считать мощность пустого множества равной .

Аналогичным образом можно определить Бесконечные нечеткие множества как такие нечеткие множества, носитель которых не является конечным множеством. При этом счетным нечетким множеством будем называть нечеткое множество со счетным носителем, т. е. носитель которого имеет счетную мощность . Несчетным нечетким множеством будем называть нечеткое множество с несчетным носителем, т. е. носитель которого имеет несчетную мощность или мощность континуума .

Рассмотрим два основных способа, которыми формально могут

Быть заданы произвольные нечеткие множества.

Список с перечислением всех элементов и соответствующих им значений функции принадлежности, образующих рассматриваемое нечеткое множество. При этом элементы с нулевыми значениями функции принадлежности в этом списке просто не указываются. Этот способ используется для задания нечетких множеств с конечным дискретным носителем и небольшим числом элементов. Как уже отмечалось, такое нечеткое множество записывают в виде , где – число элементов нечеткого множества .

Аналитическое выражение для описания соответствующей функции принадлежности. Этот способ может быть использован для задания произвольных нечетких множеств как с конечным, так и с бесконечным носителем. В этом случае нечеткое множество удобно записывать в виде , где – некоторая функция, заданная аналитически в форме математического выражения , или графически – в виде некоторой кривой. При этом вид функции целиком определяется тем, какое именно нечеткое множество эта функция должна описать.

Пример 1.3. Пусть – множество действительных чисел. Тогда нечеткое множество чисел, «близких к », можно задать функцией принадлежности, например, следующим образом:

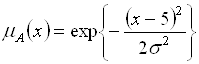(1.8)

Или

, . (1.9)

При этом численные значения параметров (в соотношении (1.8)) и (в соотношении (1.9)) выбираются в зависимости от того, как понимается нечеткий термин «Близки». Для описания множества чисел, очень близких к , следует положить равным, например, , а ; для множества чисел, не очень далеких от 5, естественно выбрать

.

Перейдем к рассмотрению основных характеристик нечетких множеств.

< Предыдущая		Следующая >