46. Закон больших чисел. Использование закона больших чисел
Рассмотрим независимые: одинаково распределенные случайные величины X1, X2, ..., Xn с конечным мат. ожиданием и дисперсией.
![]()
Рассмотрим их среднее арифметическое
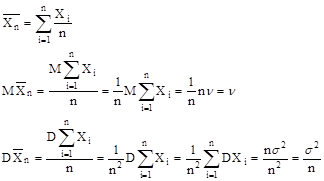
Используя вспомогательное неравенство получим
![]()
Получаем
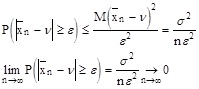
При числе испытаний, стремящихся к ¥ среднее арифметическое по вероятности сходится к математическому ожиданию.
В любом университетском учебнике доказывается сходимость с вероятностью 1.
Использование закона больших чисел.
Пусть имеется одна случайная величина X, над которой проведено n испытаний. Результаты испытаний
![]()
Тогда в силу примечания, сделанного Бернулли, эти n-чисел можно считать результатом одного испытания над n-мерной случайной величиной, у которой Xi независимы и распределены как X, т. е.
Тогда 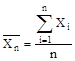 является реализацией следующего
является реализацией следующего
![]()
Для ![]() справедлив закон больших чисел, следовательно
справедлив закон больших чисел, следовательно ![]() является хорошей оценкой величины X.
является хорошей оценкой величины X.
| < Предыдущая | Следующая > |
|---|