39. Нахождение плотности вероятности суммы двух независимых случайных величин

Дискретный случай.

Пусть X и Y - две дискретные независимые величины данного испытания и Z=X+Y. Возможное значение Z=z=x+y всегда представляет сумму двух возможных значений слагаемых X=x и Y=y. По правилу сложения

Где суммирование распространено на те пары, которые в сумме дают Z. В силу независимости X и Y

Приняв во внимание, что y=z-x

Последняя сумма распространяется не на все значения x, а только на такие, для которых z-x равно одному из возможных значений y.

Если условиться, что P(y=z-x)=0, если z-x не принадлежит к числу возможных значений Y, то

Аналогично

Формулы (1) и (2) определяют композицию величин X и Y.

Или

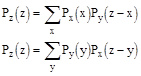
Непрерывный случай.

Пусть X и Y независимые непрерывные случайные величины. Пусть f(x, y) - двумерная плотность вероятности двумерной случайной величины XY. Плотность совместного распределения f(x, y) в силу независимости X и Y имеет вид

Рассмотрим функцию распределения случайной величины Z.

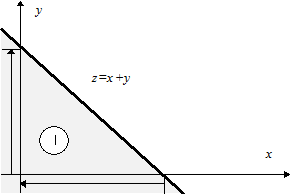
Для того, чтобы имело место событие Действительное число необходимо и достаточно, чтобы случайная точка Q(x, y) попала в область 1.

Тогда эта вероятность равна

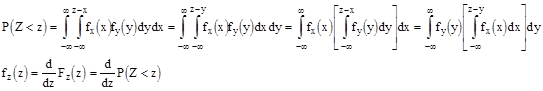
Дифференцируя под знаком интеграла

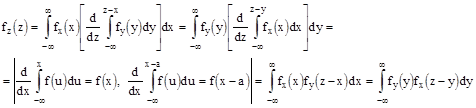
< Предыдущая		Следующая >