37. Коэффициент ковариации

Коэффициентом ковариации называется выражение

Эта формула верна, т. к. верна следующая формула.

Пусть

Тогда

Если случайные величины XY независимы, то их коэффициент ковариации равен нулю, обратное в общем случае неверно.

Пример.

X - случайная величина, имеющая нормальное распределение с нулевым мат. ожиданием

Y=X2 (Y и X связаны функционально).

Найдем

Случайная величина называется Нормированной случайной величиной, ее мат. ожидание равно 0, а дисперсия -1.

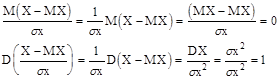
Коэффициентом корреляции случайных величин X и Y - это число

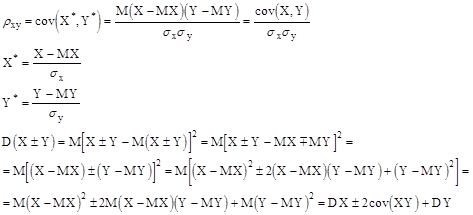
Следствие:

Если X и Y независимы, то коэффициент ковариации равен 0, то

Доказать, если независимы, то

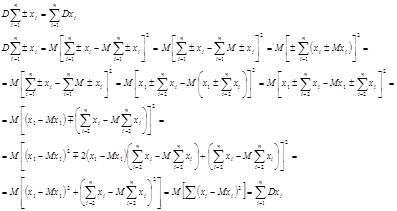
< Предыдущая		Следующая >