25. Распределение Гаусса - нормальное
Случайная величина имеет нормальное распределение (распределение Гаусса) и называется нормально распределенной, если ее плотность вероятности
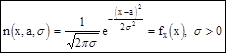
Из определения
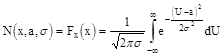
Функция распределения
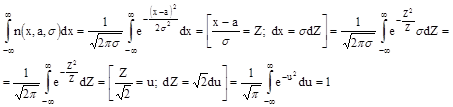
Найдем выражение для производящей функции нормального распределения
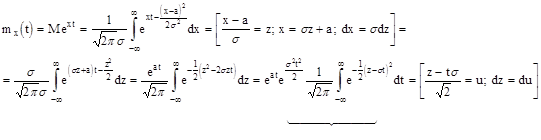
=1 (интеграл Эйлера)
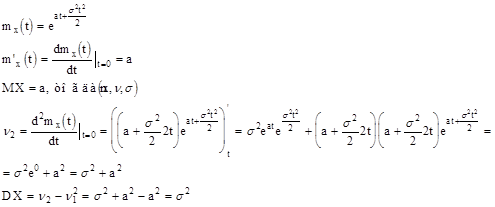
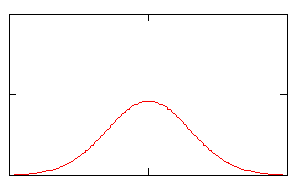
Изобразим примерный вид плотности
|
|
|
Рассмотрим центрированную нормальную величину, т. е. MX=0
![]()
У центральной нормированной величины все нечетные начальные моменты равны 0
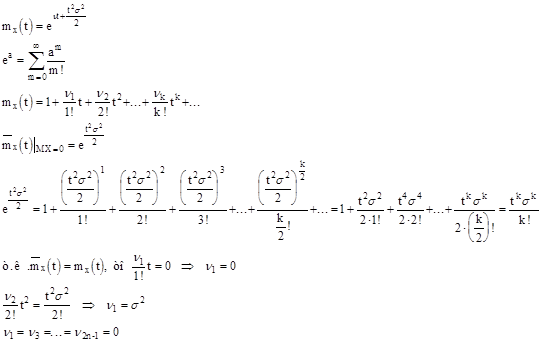
| < Предыдущая | Следующая > |
|---|