24. Вероятностные характеристики непрерывных случайных величин

Пусть имеется случайная величина, являющаяся функцией от непрерывной случайной величины X.

Y=x(x)

Математическим ожиданием непрерывной случайной величены является число:

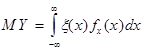, - плотность вероятности случайной величины.

Обоснование этой формулы.

Аппроксимируем непрерывную случайную величину Y случайной величены Y*, которая является дискретной. Пусть числовая ось - пространство элементарных событий случайной величены X, разобьем всю числовую ось на отрезки достаточно малой длины.

 

2n отрезков.

Если в результате испытания случайная величена X попала в отрезок с начальной вершиной xi, то случайная величена X* приняла значение x(xi) с точностью до бесконечно малой Dx - длины i-го отрезка. Вероятность того, что Y* примет значение x(xi) с точностью до бесконечно малой более высокого порядка, чем Dx, тем более точно Y* аппроксимирует Y.

Вероятность наступления x(xi) для Y* равна

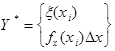
, при Эта сумма переходит в .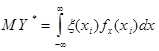

Тогда .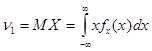

Самим показать, что все свойства мат. ожидания для дискретной случайной величены сохраняются для непрерывной случайной величены.

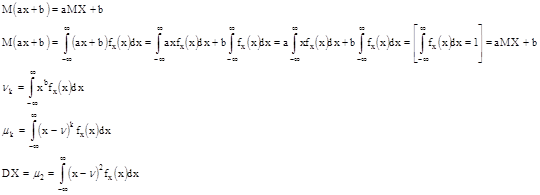
Доказать, что

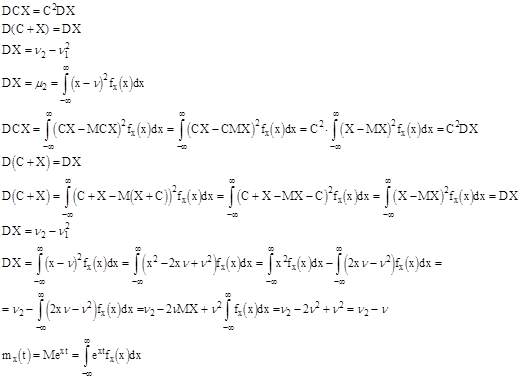
Доказать самим, что свойство 1 и 2 для производящей функции в дискретном случае справедливы и для непрерывного.

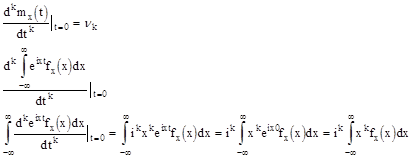
< Предыдущая		Следующая >