9.2. Функция одного случайного аргумента
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называется функцией случайного аргумента Х и записывается ![]() .
.
Если Х — дискретная случайная величина и функция ![]() монотонна, то различным значениям Х соответствуют различные значения Y, причем вероятности соответствующих значений Х и Y одинаковы:
монотонна, то различным значениям Х соответствуют различные значения Y, причем вероятности соответствующих значений Х и Y одинаковы:
![]() и
и ![]() .
.
Если же ![]() немотонная функция, то различным значениям Х могут соответствовать одинаковые значения Y. В этом случае для отыскания вероятностей возможных значений Y следует сложить вероятности тех возможных значений Х, при которых Y принимает одинаковые значения.
немотонная функция, то различным значениям Х могут соответствовать одинаковые значения Y. В этом случае для отыскания вероятностей возможных значений Y следует сложить вероятности тех возможных значений Х, при которых Y принимает одинаковые значения.
Пример 10.1. Дискретная случайная величина Х задана законом распределения
|
Х |
2 |
3 |
5 |
7 |
|
Р |
0,3 |
0,2 |
0,1 |
0,4 |
Найти закон распределения случайной величины Y, равной 2Х.
Решение. Находим возможные значения Y:
![]() ;
; ![]() ;
;![]() ;
; ![]() .
.
Так как функция ![]() монотонна, то вероятности
монотонна, то вероятности ![]() , т. е.
, т. е.
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Запишем искомый закон распределения Y
|
Y |
4 |
6 |
10 |
14 |
|
Р |
0,3 |
0,2 |
0,1 |
0,4 |
Пример 10.2. Дискретная случайная величина Х задана законом распределения
|
Х |
–3 |
–2 |
–1 |
0 |
1 |
2 |
|
Р |
0,1 |
0,2 |
0,2 |
0,1 |
0,3 |
0,1 |
Найти закон распределения случайной величины ![]() .
.
Решение. Находим возможные значения случайной величины ![]() :
:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Значения
. Значения ![]() И
И ![]() встречаются только по одному разу, а значения
встречаются только по одному разу, а значения ![]() совпадают, поэтому вероятность того, что
совпадают, поэтому вероятность того, что ![]() , будет равна сумме вероятностей 0,2 + 0,1 = 0,3. Аналогично,
, будет равна сумме вероятностей 0,2 + 0,1 = 0,3. Аналогично, ![]() , поэтому
, поэтому ![]() .
.
Напишем искомый закон распределения Y, расположив значения Y в порядке возрастания
|
Y |
0 |
1 |
4 |
9 |
|
Р |
0,1 |
0,5 |
0,3 |
0,1 |
Если Х — непрерывная случайная величина, заданная плотностью распределения ![]() , и если
, и если ![]() — дифференцируемая строго монотонная функция, обратная функция которой
— дифференцируемая строго монотонная функция, обратная функция которой ![]() , то плотность распределения
, то плотность распределения ![]() случайной величины Y находят из равенства
случайной величины Y находят из равенства
![]() .
.
Если функция ![]() в интервале возможных значений Х не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция
в интервале возможных значений Х не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция ![]() монотонна, и найти плотности распределения
монотонна, и найти плотности распределения ![]() для каждого интервала монотонности, а затем представить
для каждого интервала монотонности, а затем представить ![]() в виде суммы
в виде суммы
![]() .
.
Пример 10.3. Задана плотность распределения ![]() случайной величины Х, возможные значения которой заключены в интервале
случайной величины Х, возможные значения которой заключены в интервале ![]() . Найти плотность распределения случайной величины
. Найти плотность распределения случайной величины ![]() .
.
Решение. Так как функция ![]() дифференцируемая и строго возрастает, то применима формула
дифференцируемая и строго возрастает, то применима формула ![]() , где
, где ![]() — функция, обратная функции
— функция, обратная функции ![]() .
.
Находим ![]() :
: ![]() . Тогда
. Тогда 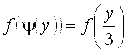 ,
, ![]() . Искомая плотность распределения
. Искомая плотность распределения ![]() . Так как Х изменяется в интервале
. Так как Х изменяется в интервале ![]() и У = 3Х, то
и У = 3Х, то ![]() .
.
Ответ: ![]() ,
, ![]() .
.
Пример 10.4. Случайная величина Х распределена по закону Коши
 .
.
Найти плотность распределения случайной величины ![]() .
.
Решение. Функция ![]() монотонно возрастающая при всех
монотонно возрастающая при всех ![]() . Находим обратную функцию
. Находим обратную функцию ![]() :
: ![]() . Тогда
. Тогда
 ,
,  ,
,  .
.
Следовательно,

Ответ:  .
.
Пример 10.5. Задана плотность  Нормально распределенной случайной величины Х. Найти плотность распределения
Нормально распределенной случайной величины Х. Найти плотность распределения ![]() Случайной величины
Случайной величины ![]() .
.
Решение. Так как в интервале ![]() функция
функция ![]() не монотонна, то разобъем этот интервал на интервалы
не монотонна, то разобъем этот интервал на интервалы ![]() И
И ![]() , в которых она монотонна. В интервале
, в которых она монотонна. В интервале ![]() Обратная функция
Обратная функция ![]() , в интервале
, в интервале ![]()
![]() ,
, 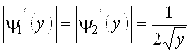 ,
,  ,
,  .
.
Искомую плотность распределения находим из равенства
![]() ,
,
 .
.
Так как ![]() , причем
, причем ![]() , то
, то ![]() . Таким образом, в интервале
. Таким образом, в интервале ![]() искомая плотность распределения
искомая плотность распределения  , вне этого интервала
, вне этого интервала ![]() .
.
Ответ:  при
при ![]() ,
, ![]() при
при ![]() .
.
| < Предыдущая | Следующая > |
|---|