8.7. Задачи для самостоятельного решения

8.44. Случайная величина Х распределена по показательному закону

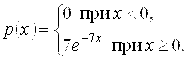
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и функцию распределения этой случайной величины. Найти вероятность попадания значений случайной величины Х в интервал .

Ответ: ;

.

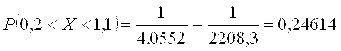8.45. Среднее время безотказной работы прибора равно 85 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч прибор не выйдет из строя.

Ответ: а) ;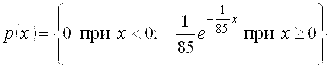

;

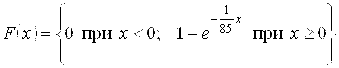Б) .

8.46. Найти эксцесс показательного распределения.

Ответ: .

8.47. Производится испытание трех элементов, работающих независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента ; для второго — для третьего элемента Найти вероятности того, что в интервале времени  часов откажут: а) только один элемент; б) только два элемента; в) хотя бы один элемент; г) все три элемента; д) не менее двух элементов.

Ответ: а) 0,069; б) 0,4172; в) 0,9975; г) 0,511; д) 0,928.

8.48. Р %-м ресурсом элемента называется такое число T, что за время T элемент не выходит из строя с вероятностью Р. Считается, что время T непрерывной работы электрической лампочки распределено по показательному закону. Найти вероятность того, что лампочка будет гореть в течение 2 лет, если ее 90 %-й ресурс составляет 6 мес.

Ответ: .

8.49. Срок службы жесткого диска компьютера – случайная величина, подчиняющаяся экспоненциальному распределению со средней в 12 000 часов. Найти долю жестких дисков, срок службы которых превысит 20 000 часов.

Ответ: .

8.50. Срок службы батареек для слуховых аппаратов приблизительно подчиняется экспоненциальному закону с . Какова доля батареек со сроком службы больше чем 9 дней?

Ответ: .

8.51. Служащий рекламного агентства утверждает, что время, в течение которого телезрители помнят содержание коммерческого рекламного ролика, подчиняется экспоненциальному закону с Дня. Найти долю зрителей, способных вспомнить рекламу спустя 7 дней.

Ответ: .

8.52. Компьютерный программист использует экспоненциальное распределение для оценки надежности своих программ. После того, как он нашел 10 ошибок, он убедился, что время (в днях) до нахождения следующей ошибки подчиняется экспоненциальному распределению с . Найти среднее время, потраченное для нахождения первой ошибки; определить вероятность того, что для нахождения первой ошибки понадобится более 5 дней; найти вероятность того, что на нахождение одиннадцатой ошибки потребуется от 3 до 10 дней.

Ответ: М (Х) = 4; ; .

8.53. Случайная величина Х распределена по показательному закону: Р(Х) = = 0 при Х < 0, При . Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и функцию распределения этой случайной величины. Найти вероятность попадания случайной величины Х в интервал (0,2; 1,1).

Ответ: М (Х) = 1/6; ; ; ;

.

< Предыдущая		Следующая >