8.6. Показательный (экспоненциальный) закон распределения

Непрерывная случайная величина Х имеет Показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид

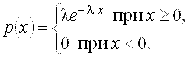
Функция распределения случайной величины, распределенной по показательному закону, равна

Кривая распределения Р(Х) и график функции распределения приведены на рис. 8.13.

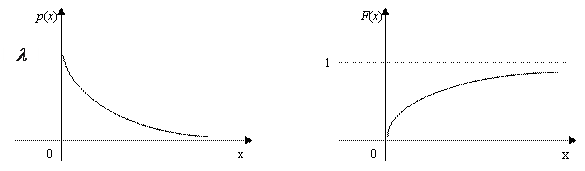
Рис. 8.13

Для случайной величины, распределенной по показательному закону

; .

Вероятность попадания в интервал непрерывной случайной величины Х, распределенной по показательному закону

.

Замечание. Показательный закон распределения вероятностей встречается во многих задачах, связанных с простейшим потоком событий. Под Потоком событий понимают последовательность событий, наступающих одно за другим в случайные моменты. Например, поток вызовов на телефонной станции, поток заявок в системе массового обслуживания и др.

Пример 8.18. Непрерывная величина Х распределена по показательному закону

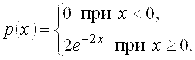
Найти вероятность попадания значений величины Х в интервал .

Решение. Поскольку , то

Пример 8.19. Записать плотность распределения и функцию распределения показательного закона, если параметр . Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной по этому закону.

Решение. Так как , то плотность распределения

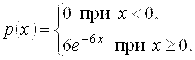
Функция распределения имеет вид

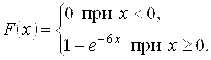
Поскольку для показательного закона

; ,

А по условию , то

.

Пример 8.20. Установлено, что время ремонта магнитофонов есть случайная величина Х, распределенная по показательному закону. Определить вероятность того, что на ремонт магнитофона потребуется не менее 15 дней, если среднее время ремонта магнитофонов составляет 12 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины Х.

Решение. По условию математическое ожидание , откуда параметр . Тогда плотность вероятности и функция распределения имеют вид: ; . Искомую вероятность можно найти, интегрируя плотность вероятности, т. е.

,

Но проще использовать функцию распределения

.

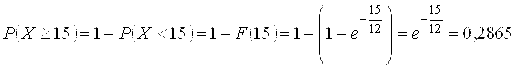Среднее квадратическое отклонение Дней.

Пример 8.21. Найти асимметрию показательного распределения.

Решение. Так как асимметрия 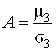, а , то найдем вначале центральный момент третьего порядка

:

Найдем

.

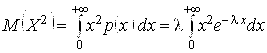Интегрируя дважды по частям, получим

.

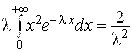Аналогично рассчитаем

.

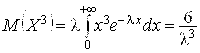Следовательно,

.

Значит,

.

Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого определяет Вероятность отказа элемента за время длительностью T. Здесь Т — длительность времени безотказной работы элемента,  — интенсивность отказов (среднее число отказов в единицу времени).

Функция надежности определяет вероятность безотказной работы элемента за время длительностью T.

Пример 8.22. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента ; для второго ; для третьего элемента Найти вероятности того, что в интервале времени  часов откажут: а) только один элемент; б) только два элемента; в) все три элемента.

Решение. А) Вероятность отказа первого элемента

;

Второго элемента

;

Третьего элемента

.

Следовательно, искомая вероятность

.

Б) .

В) .

< Предыдущая		Следующая >