6.3. Теоремы Муавра-Лапласа

Теорема 2 (Муавра-Лапласа (локальная)). Если вероятность наступления события А в каждом из n независимых испытаниях равна Р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в N испытаниях событие А наступит раз, приближенно равна (чем больше N, тем точнее) значению функции

,

Где , 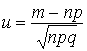. Таблица значений функции приведена в прил. 1.

Пример 6.5. Вероятность найти белый гриб среди прочих равна . Какова вероятность того, что среди 300 грибов белых будет 75?

Решение. По условию задачи , . Находим . По таблице находим .

.

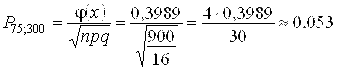Ответ: .

Теорема 3 (Муавра-Лапласа (интегральная)). Если вероятность наступления события А в каждом из N независимых испытаний равна Р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в N испытаниях число успехов M находится между и , приближенно равна (чем больше N, тем точнее)

,

Где Р — вероятность появления успеха в каждом испытании, , , 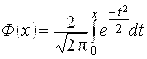значения приведены в прил. 2.

Пример 6.6. В партии из 768 арбузов каждый арбуз оказывается неспелым с вероятностью . Найти вероятность того, что количество спелых арбузов будет в пределах от 564 до 600.

Решение. По условию По интегральной теореме Лапласа

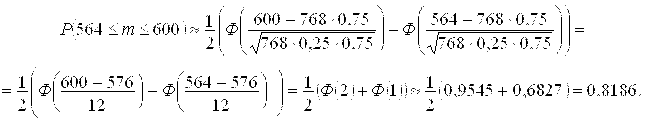
Ответ:

Пример 6.7. Город ежедневно посещает 1000 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы с вероятностью приблизительно 0,99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно быть для этого в его ресторане?

Решение. Пусть А = «турист пообедал у заинтересованного владельца». Наступление события А будем считать «успехом», , . Нас интересует такое наименьшее число K, что вероятность наступления не менее чем K «успехов» в последовательности из Независимых испытаний с вероятностью успеха Р = 0,5 приблизительно равна 1 – 0,99 = 0,01. Это как раз вероятность переполнения ресторана. Таким образом, нас интересует такое наименьшее число K, что . Применим интегральную теорему Муавра-Лапласа

Откуда следует, что

.

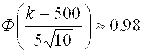Используя таблицу для Ф(Х) (прил. 2), находим , значит . Следовательно, в ресторане должно быть 537 мест.

Ответ: 537 мест.

Из интегральной теоремы Лапласа можно получить формулу

.

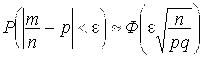Пример 6.8. Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,04.

Решение. По условию

Требуется найти вероятность 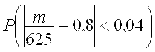. Воспользуемся формулой

.

.

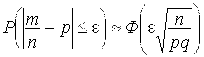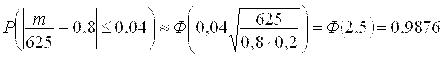Ответ: Р = 0,9876.

Пример 6.9. Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний N, при котором с вероятностью 0,7698 можно ожидать, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.

Решение. По условию 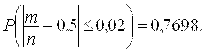Воспользуемся формулой

.

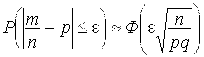Следовательно,

.

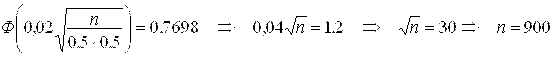Ответ: .

< Предыдущая		Следующая >