2.3. Задачи для самостоятельного решения
2.1. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность, что получится слово «два»?
Ответ: ![]() .
.
2.2. а) Три одноклассника Иванов, Петров и Сидоров решили подать документы на экономический факультет одного из четырех вузов: БГУ, БНТУ, БГАТУ и БГУИР, причем каждый выбирал себе вуз случайно и независимо от других. Найти вероятности следующих событий:
1) всех одноклассники окажутся в разных вузах;
2) все подадут документы в один и тот же вуз;
3) все подадут документы в БГУ.
б) Студенты из общежития закупят партию из 10 арбузов в том случае, если при нарезке двух из них, выбранных случайным образом, оба окажутся зрелыми. Какова вероятность того, что студенты купят арбузы, среди которых будет 4 незрелых?
в) На одной полке наугад расставляются N различных книг. Найти вероятность того, что две определенные книги окажутся поставленными рядом (в любом порядке). Задачу решить в общем виде и вычислить конкретный ответ для ![]() ,
, ![]() ,
, ![]() .
.
Ответ: А) 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
б) ![]() ;
;
в) ![]() , если
, если ![]() , то
, то ![]() ; если
; если ![]() , то
, то ![]() ;
;
если ![]() , то
, то ![]() .
.
2.3. Имеется пять отрезков, длины которых равны соответственно 1, 3, 5, 7 и 9 единицам. Определить вероятность того, что с помощью взятых наудачу трех отрезков из данных пяти можно построить треугольник.
Ответ: 0,3.
2.4. Из восьми магазинов с номерами 1,2, …, 8 для проверки выбирают три. Какова вероятность того, что будут проверяться магазины № 5 и № 6?
Ответ: ![]() .
.
2.5. Имеется 6 карточек с буквами А, А, Т, Т, Л, Н. Карточки перемешиваюти затем наугад достают по очереди и располагают в ряд в порядке появления. Какова вероятность, что получится слово «АТЛАНТ»?
Ответ: ![]() .
.
2.6. На пяти карточках написаны цифры от 1 до 5. Опыт состоит в случайном выборе трех карточек и раскладывании их в порядке поступления в ряд слева направо. Найти вероятность следующих событий: А = {появится число 123}; В = {появится число, не содержащее цифры 2}; С = {появится число, состоящее из последовательных цифр}.
Ответ: ![]() .
.
2.7. Десять человек входят в комнату, где имеется всего 7 стульев, и рассаживаются случайным образом, но так, что все стулья оказываются занятыми. Какова вероятность того, что а) два определенных лица окажутся без места? б) 4 определенных лица будут сидеть?
Ответ: А) ![]() ; б)
; б) ![]() .
.
2.8. Фирмы А1, А2, А3, А4, А5 предлагают свои условия по выполнению 3 различных контрактов С1, С2, С3. Любая фирма может получить только один контракт. Если предположить равновозможность заключения контрактов, чему равна вероятность того, что фирма А3 получит контракт? Чему равна вероятность того, что фирмы А1 и А2 получат контракт?
Ответ: ![]() ;
; ![]() .
.
2.9. 8 вариантов контрольной работы, написанные каждый на отдельной карточке, перемешиваются и распределяются случайным образом среди шести студентов, сидящих в одном ряду, причем каждый получает по одному варианту. Найти вероятность следующих событий: А = «варианты с номерами 1 и 2 останутся неиспользованными»; В = «варианты 1 и 2 достанутся рядом сидящим студентам»; С = «будут распределены последовательные номера вариантов».
Ответ: ![]() .
.
2.10. А и В и еще 8 человек стоят в очереди. Определить вероятность того, что А и В отделены друг от друга тремя лицами.
Ответ: ![]() .
.
2.11. Группа, состоящая из 6 человек, занимает места с одной стороны прямоугольного стола. Найти вероятность того, что два определенных лица окажутся рядом, если а) число мест равно 6; б) число мест равно 8.
Ответ: а) ![]() ; б)
; б) ![]() .
.
2.12. В течение пяти дней случайным образом поступают сообщения о банкротстве одного из пяти банков, назовем их условно А, В, С, D, Е. Чему равна вероятность того, что сообщение о банкротстве банка В не следует сразу же за сообщением о банкротстве банка А?
Ответ: ![]() .
.
2.13. Пять мужчин и пять женщин случайным образом рассаживаются в ряд на десять мест. Найти вероятности следующих событий: А = «никакие два мужчины не будут сидеть рядом»; В = «все мужчины будут сидеть рядом», С = «мужчины и женщины будут чередоваться».
Ответ: ![]() .
.
2.14. В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятности следующих событий: А = «все пассажиры выйдут на четвертом этаже»; В = «все пассажиры выйдут одновременно (на одном и том же этаже)»; С = «все пассажиры выйдут на разных этажах».
Ответ: ![]() .
.
2.15. 9 пассажиров наудачу рассаживаются в трех вагонах. Найти вероятность того, что а) в каждый вагон сядут по три пассажира; б) в один вагон сядут 4, в другой – 3, в третий – 2 пассажира.
Ответ: ![]()
2.16. Для доступа в компьютерную сеть оператору необходимо набрать пароль из 4 цифр. Оператор забыл или не знает необходимого кода. С какой вероятностью можно открыть замок с первой попытки, если а) все цифры в коде не повторяются; б) если повторяются?
Ответ: 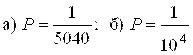 .
.
2.17. Телефонная книга раскрывается наудачу и выбирается случайный номер телефона. Считая, что телефонные номера состоят из 7 цифр, причем все комбинации цифр равновероятны, найти вероятности следующих событий: А = = «четыре последние цифры телефонного номера одинаковы»; В = «все цифры различны»; С = «номер начинается с цифры 5»; D = «номер содержит три цифры 7, две цифры 5 и две цифры 3».
Ответ: ![]() .
.
2.18. К четырехстороннему перекрестку с каждой стороны подъехало по одному автомобилю. Каждый автомобиль может с равной вероятностью совершить один из четырех маневров на перекрестке: развернуться и поехать обратно, поехать прямо, налево или направо. Через некоторое время все автомобили покинули перекресток. Найти вероятности следующих событий: А = «все автомобили поедут по одной и той же улице»; В = «по определенной улице поедут ровно три автомобиля»; С = «по крайней мере по одной из улиц не поедет ни один автомобиль».
Ответ: ![]() .
.
2.19. В партии из 15 изделий 4 бракованных. Из партии выбираются наугад 6 изделий. Определить вероятность того, что среди этих 6 изделий 2 бракованных.
Ответ: ![]() .
.
2.20. Профессор вызвал через старосту на обязательную консультацию трех студентов из шести отстающих. Староста забыл фамилии вызванных студентов и послал наудачу трех отстающих студентов. Какова вероятность того, что староста послал именно тех студентов, которых назвал профессор?
Ответ: ![]() .
.
2.21. В группе 20 студентов, среди которых 6 отличников. По списку наудачу отобраны 5 студентов. Найти вероятности следующих событий: А = «среди отобранных – нет отличников»; В = «среди отобранных – 2 отличника»; С = = «среди отобранных – хотя бы один отличник».
Ответ: ![]() .
.
2.22. Для уменьшения общего количества игр 20 команд спортсменов по жребию разбиваются на две подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся: а) в разных подгруппах; б) в одной подгруппе.
Ответ: а) Р = ![]() ; б) Р =
; б) Р = ![]() .
.
2.23. Два одинаковых по силе противника играют матч из 8 партий в теннис. Каждая партия заканчивается выигрышем либо проигрышем одного из участников. Все исходы данного матча считаются равновероятными. Найти вероятность того, что первый игрок выиграет ровно пять партий.
Ответ: ![]() .
.
2.24. В шкафу находится 10 пар ботинок различных сортов. Из них случайно выбираются 4 ботинка. Найти вероятность того, что среди выбранных отсутствуют парные.
Ответ: ![]() .
.
2.25. В библиотеке имеются книги по экономике, математике, физике, всего по 16 разделам науки. Поступили четыре заказа на литературу. Считая, что любой состав заказанной литературы равновозможен, найти вероятности следующих событий: А = «заказаны книги из различных разделов науки»; В = «заказаны книги из одного и того же раздела науки».
Ответ: ![]() .
.
2.26. В кондитерском отделе магазина имеются 9 видов шоколадных конфет. Очередной покупатель выбил чек на 500 г конфет. Найти вероятность того, что покупатель заказал: а) по 100 г конфет различного вида; б) 200 г конфет одного вида и 300 г другого; в) все конфеты одного вида.
Ответ: ![]()
2.27. 20 футбольных команд, среди которых 4 призера предыдущего первенства, по жеребьевке разбиваются на четыре занумерованные подгруппы по 5 команд. Найти вероятности следующих событий: А = «в первую и вторую подгруппы не попадет ни один из призеров»; В = «в каждую подгруппу попадет один из призеров».
Ответ: ![]() .
.
2.28. На карточках отдельно написаны буквы: А — на двух карточках; С — на 2; И — на 2; К — на 1; Т — на 3 карточках. Ребенок берет карточки в случайном порядке и прикладывает их одну к другой. Найти вероятность того, что в результате получится слово «статистика».
Ответ: 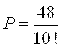 .
.
2.29. 7 яблок, 3 апельсина и 5 лимонов раскладываются случайным образом в три пакета, но так, чтобы в каждом пакете было одинаковое количество фруктов. Найти вероятности следующих событий: А = «в каждом пакете по одному апельсину»; В = «случайно выбранный пакет не содержит апельсинов».
Ответ: ![]()
2.30. Из колоды карт (36) случайным образом достают две. Найти вероятности того, что они разной масти.
Ответ: ![]()
| < Предыдущая | Следующая > |
|---|