2.2. Классическое определение вероятности

Классической схемой, или схемой случаев, называется испытание, при котором число элементарных исходов конечно и все из них равновозможны.

Элементарное событие (исход) ω называется благоприятствующим событию А, если его появление влечет наступление события А (т. е. ω входит в число элементов, составляющих А).

Классической вероятностью события А называется отношение числа M элементарных событий, благоприятствующих событию А, к числу N всех элементарных событий этой схемы

.

Из определения вероятности следует, что Р (Ø) = 0, и .

Пример 2.7. В магазин поступило 40 новых цветных телевизоров, среди которых 7 имеют скрытые дефекты. Наудачу отбирается один телевизор для проверки. Какова вероятность, что он не имеет скрытых дефектов?

Решение. Число телевизоров, не имеющих скрытых дефектов, равно . Число всех элементарных исходов всех поступивших телевизоров равно . Следовательно, по классическому определению вероятности вероятность того, что отобранный телевизор не имеет скрытых дефектов (событие А), равна

.

Ответ: Р(А) = 0,825.

Пример 2.8. 1 сентября на первом курсе одного из факультетов запланированы по расписанию три лекции из 10 различных предметов. Студент, не успевший ознакомиться с расписанием, пытается его угадать. Какова вероятность успеха в данном эксперименте, если считать, что любое расписание из трех предметов равновозможно.

Решение. Студенту необходимо из 10 лекций, которые могут быть поставлены в расписание, причем в определенном порядке, выбрать три. Следовательно, число всех возможных исходов испытания равно числу размещений из 10 по 3, т. е.

.

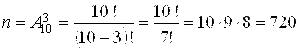Благоприятный же случай только один, т. е. M = 1. Искомая вероятность будет равна

.

Ответ: .

Пример 2.9. В подъезде дома установили замок с кодом. Дверь автоматически отпирается, если в определенной последовательности набрать три цифры из возможных десяти. Некто вошел в подъезд и, не зная кода, стал наудачу пробовать различные комбинации из трех цифр. На каждую попытку он тратит 15 секунд. Какова вероятность события А = {вошедшему удастся открыть дверь за один час}?

Решение. Так как цифры, входящие в набираемый номер, могут повторяться и порядок их набора играет существенную роль, то мы приходим к схеме размещений с повторениями. Число возможных вариантов набора трех цифр из 10 возможных равно За один час, тратя на набор комбинации 15 секунд, можно набрать 240 различных комбинаций, т. е. M = 240. Искомая вероятность

Ответ:

Пример 2.10. Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года.

Решение. Так как каждый из 12 человек может родиться в любом из 12 месяцев года, то число всех возможных вариантов можно посчитать по формуле размещений с повторениями

Число благоприятных случаев получим, переставляя месяцы рождения у этих 12 человек, т. е.

.

Тогда искомая вероятность будет равна

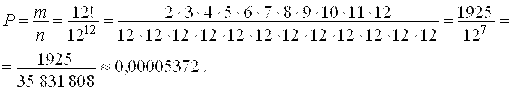
Ответ:

Пример 2.11. На полке стоят 15 книг, 5 из них в переплете. Берут наудачу три книги. Какова вероятность того, что все три книги в переплете?

Решение. Опыт состоит в том, что из 15 книг отбирают 3, причем в каком порядке они отобраны, роли не играет. Следовательно, число возможных способов выбора будет равно числу сочетаний из 15 по 3, т. е.

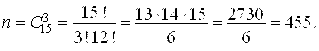
Число благоприятных случаев будет равно числу сочетаний из 5 по 3, т. е.

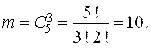
Искомая вероятность

Ответ:

Пример 2.12. В кондитерской имеются 6 видов пирожных. Очередной покупатель выбил чек на 3 пирожных. Считая, что любой заказываемый набор пирожных равновероятен, вычислить вероятность того, что покупатель заказал пирожные разных видов.

Решение. Число всех возможных видов заказов 3 пирожных будет равно числу сочетаний с повторениями из 6 элементов по 3, т. е.

Число благоприятных случаев будет равно числу сочетаний из 6 по 3, т. е.

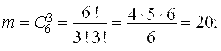
Ответ:

Пример 2.13. Десять приезжих мужчин, среди которых Петров и Иванов, размещаются в гостинице в двух трехместных и одном четырехместном номерах. Какова вероятность события А, состоящего в том, что Петров и Иванов попадут в четырехместный номер?

Решение. Число всех возможных размещений 10 человек в двух трехместных и одном четырехместном номере равно числу перестановок из десяти элементов, среди которых 3 одного вида, 3 другого и 4 третьего, т. е.

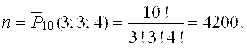
После того как Иванов и Петров будут размещены в четырехместном номере, остальные 8 человек должны быть размещены в двух трехместных и на оставшиеся два свободных места в четырехместном номере, это можно будет сделать следующим образом:

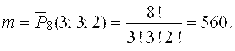
Искомая вероятность

Ответ:

< Предыдущая		Следующая >