Тема 6.1. Упражнения

1) Вычислить числовые характеристики показательного распределения. Найти вероятность того, что случайная величина примет значение меньшее, чем ее математическое ожидание.

2) В нашем распоряжении имеется 5 лампочек, каждая из них с вероятностью 0.4 имеет дефект. Лампочка ввинчивается в патрон, и включается ток. При включении тока дефектная лампочка сразу перегорает, после чего заменяется другой. Построить распределение числа испробованных лампочек и найти числовые характеристики.

3) Функция распределения непрерывной случайной величины имеет вид: . Найти числовые характеристики этой случайной величины.

4) Определить числовые характеристики случайной величины, распределенной по закону Пуассона.

5) Производится ряд независимых опытов, в каждом из которых может появиться некоторое событие А. Вероятность события А в каждом опыте равна Р. Опыты производятся до первого появления события А, после чего они прекращаются. Случайная величина X – число произведенных опытов. Построить ряд распределения этой случайной величины и найти ее математическое ожидание и дисперсию.

6) Производится два независимых выстрела по мишени. Вероятность попадания при каждом выстреле равна Р. Рассматриваются случайные величины: X – разность между числом попаданий и числом промахов; H – сумма числа попаданий и числа промахов. Построить для каждой из случайных величин X и H ряд распределения. Найти их числовые характеристики.

7) Случайная величина подчинена закону распределения с плотностью . Найти характеристики этой случайной величины.

8) Автомашина проходит техосмотр и техобслуживание. Число неисправностей, обнаруженных во время техосмотра, распределено по закону Пуассона с параметром L. Если неисправностей не обнаружено, техобслуживание продолжается в среднем 2 часа. Если обнаружены 1 или 2 неисправности, то на устранение каждой из них тратится в среднем еще полчаса. Если обнаружено более 2 неисправностей, то машина ставится на профилактический ремонт, где она находится в среднем 4 часа. Определить закон распределения среднего времени Т обслуживания и ремонта машины и его математическое ожидание.

9) Найти математическое ожидание и дисперсию случайной величины, заданной плотностью распределения:

а) 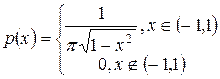; б) .

< Предыдущая		Следующая >