Тема 6. Числовые характеристики случайных величин. Теоретические сведения

Математическим ожиданием Дискретной случайной величины называется число: . Математическим ожиданием непрерывной случайной величины с плотностью называется число 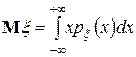. Если вероятностная мера определяется функцией распределения, то .

Свойства математического ожидания:

1. , то .

2. : .

3. .

4. 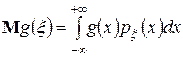. В частности, .

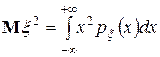5. Для независимых случайных величин : .

Дисперсией Случайной величины называется число . Иногда для вычислений более удобна формула . Величина называется Среднеквадратичным Отклонением значений случайной величины от ее среднего.

Свойства дисперсии:

1. . В частности, , то .

2. .

3.Для независимых случайных величин : .

Начальным моментом k-го порядка случайной величины называется математическое ожидание K-й степени этой случайной величины: . Для дискретной: 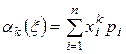, для непрерывной: .

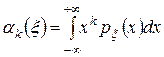Центральным моментом k-го порядка Случайной величины называется математическое ожидание K-й степени соответствующей центрированной случайной величины: . Для дискретной величины: 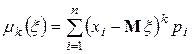, а для непрерывной: .

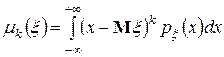Коэффициентом асимметрии или Асимметрией распределения называется величина 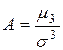. Эксцессом случайной величины называется отношение .

< Предыдущая		Следующая >