23. Дисперсия случайной величины
Дисперсия DX случайной величины x определяется формулой
DX = M(x – MX)2
Дисперсия случайной величины — это математическое ожидание квадрата отклонения случайной величины от её математического ожидания.
Рассмотрим случайную величину x с законом распределения
|
X |
1 |
2 |
3 |
|
Р |
|
|
|
Вычислим её математическое ожидание.
MX = 1×![]() + 2×
+ 2×![]() + 3×
+ 3×![]() =
= ![]()
Составим закон распределения случайной величины x – MX
|
X– MX |
|
|
|
|
Р |
|
|
|
А затем закон распределения случайной величины (x – MX)2
|
(x– MX)2 |
|
|
|
|
Р |
|
|
|
Теперь можно рассчитать величину DX :
DX = ![]() ×
×![]() +
+ ![]() ×
×![]() +
+ ![]() ×
×![]() =
= ![]()
Используя определение дисперсии, для дискретной случайной величины формулу вычисления дисперсии можно представить в таком виде:
DX = 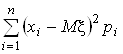
Можно вывести ещё одну формулу для вычисления дисперсии:
DX = 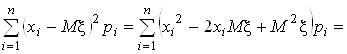
= 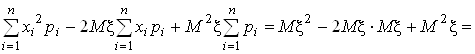
= MX2 – M2x
Таким образом, дисперсия случайной величины равна разности математического ожидания квадрата случайной величины и квадрата её математического ожидания.
Пример.
Найти дисперсию случайной величины, заданной законом распределения
|
X |
1 |
0 |
|
Р |
P |
Q |
Выше было показано, что MX = Р. Легко видеть, что MX2 = Р. Таким образом, получается, что DX = Р – Р2 = Pq.
Дисперсия характеризует степень рассеяния значений случайной величины относительно её математического ожидания. Если все значения случайной величины тесно сконцентрированы около её математического ожидания и большие отклонения от математического ожидания маловероятны, то такая случайная величина имеет малую дисперсию. Если значения случайной величины рассеяны и велика вероятность больших отклонений от математического ожидания, то такая случайная величина имеет большую дисперсию.
Свойства дисперсии.
1. Если K – число, то D(KX) = K2 DX.
Доказательство.
D(KX) = M(KX – M(KX))2 = M(KX – K MX)2 = M(K2 (x – MX)2) = K2M(x – MX)2 =
= K2 DX
2. Для попарно независимых случайных величин x1, x2,¼, xN справедливо равенство
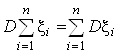
Это свойство оставим без доказательства. Рекомендуем читателю рассмотреть следующий пример.
Пусть x и h – независимые случайные величины с заданными законами распределения:
|
X |
0 |
1 |
H |
1 |
2 | |
|
Р |
0,25 |
0,75 |
Р |
0,7 |
0,7 |
Показать, что D(x + h) = DX + DH.
| < Предыдущая | Следующая > |
|---|