22. Математическое ожидание случайной величины
Пусть задан закон распределения случайной величины x.
|
X |
Х1 |
Х2 |
Х3 |
¼ |
Хn |
|
P |
P1 |
P2 |
P3 |
¼ |
Pn |
Математическое ожидание МX (или М(x)) случайной величины x определяется формулой
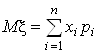
Рассмотрим пример. Пусть в некотором магазине, торгующем электробытовой техникой, получены статистические данные о числе проданных холодильников в каждый день месяца (условно считаем, что месяц состоит из 30 рабочих дней). Эти данные собраны в таблицу
|
Количество проданных холодильников |
0 |
1 |
2 |
3 |
4 |
5 |
|
Число дней, в которые было продано столько холодильников |
3 |
7 |
8 |
9 |
2 |
1 |
По этой таблице легко подсчитать число холодильников, проданных в магазине за месяц: 0*1+1*7+2*8+3*9+4*2+5*1 = 63. Чтобы подсчитать среднее число холодильников, продававшихся в один день месяца, нужно эту сумму разделить на 30, в результате получим 2,1. Если в приведенной таблице каждое число второй строки поделить на 30, то получится последовательность дробей
![]() ,
,
Каждая из которых представляет собой так называемую Относительную частоту, с которой в данный месяц появлялся приведенный в верхней строке объём продаж. Очевидно, что если просуммировать все произведения чисел, стоящих в первой строке таблицы, на их относительные частоты, то получится то же среднее число продававшихся в один день холодильников:
![]()
Если бы в последней формуле относительные частоты рассчитывались не для одного месяца, а для существенно большего срока, то при некоторых условиях (например, при отсутствии кризисных явлений, существенно влияющих на спрос населения на дорогостоящие товары) эти относительные частоты можно было бы считать довольно близкими к вероятностям соответствующих значений объёма продаж. Таким образом, приходим к выводу, что математическое ожидание случайной величины – это в некотором смысле её среднее значение. Следует отметить, что случайная величина может вообще не принимать значения, равного её математическому ожиданию. Так, например, случайная величина, принимающая только значения 1 и –1, каждое – с вероятностью 0,5, имеет математическое ожидание, равное нулю.
Пример. Найти математическое ожидание случайной величины, заданной законом распределения
|
X |
1 |
0 |
|
Р |
P |
Q |
Здесь p + q = 1.
Mx = 1×р + 0×q = р
Свойства математического ожидания.
1. Если случайная величина x принимает одно и то же значение при всех исходах случайного эксперимента, то есть x º С, то её математическое ожидание равно С.
2. Если МX = А, и K – константа, то М(KX) = KMX (математическое ожидание случайной величины, умноженной на число, равно математическому ожиданию случайной величины, умноженному на это число).
3. Если МX = А, и K – константа, то М(K + X) = K + MX (математическое ожидание суммы случайной величины и числа равно сумме этого числа и математического ожидания случайной величины).
Выведем формулу для математического ожидания суммы двух случайных величин x и h, определённых на одном и том же пространстве элементарных исходов и заданных законами распределения
|
X |
Х1 |
¼ |
XN |
H |
Y1 |
¼ |
Yk | |
|
Р |
|
¼ |
|
Р |
|
¼ |
|
М(x + h) = (Х1 + У1)Р((x = Х1) ∩ (h = У1))+ (Х2 + У1)Р((x = Х2) ∩ (h = У1)) +¼
+(ХI + УJ)Р((x = ХI) ∩ (h = УJ)) + ¼ + (ХN + УK)Р((x = ХN) ∩ (h = УK))
Очевидно, что сумма в правой части последней формулы содержит Nk Слагаемых. Преобразуем эту сумму следующим образом:
М(x + h) = Х1 Р((x=Х1)∩(h=У1)) + Х1 Р((x=Х1)∩(h=У2)) +¼+Х1 Р((x=Х1)∩(h=УK)) + + Х2Р((x=Х2)∩(h=У1)) + Х2Р((x=Х2)∩(h=У2)) +¼ + Х2Р((x=Х2)∩(h=УK)) + ¼
+ ХNР((x=ХN)∩(h=У1)) + ХNР((x=ХN)∩(h=У2)) +¼ + ХNР((x=ХN)∩(h=УK)) +
+ У1Р((x=Х1)∩(h=У1)) + У1Р((x=Х2)∩(h=У1)) +¼ + У1Р((x=ХN)∩(h=У1)) +
+ У2Р((x=Х1)∩(h=У2)) + У2Р((x=Х2)∩(h=У2)) +¼ + У2Р((x=ХN)∩(h=У2)) + ¼
+ УKР((x=Х1)∩(h=УK)) + УKР((x=Х2)∩(h=УK)) +¼ + УKР((x=ХN)∩(h=УK)) =
= Х1(Р((x=Х1)∩(h=У1)) + Р((x=Х1)∩(h=У2)) +¼ + Р((x=Х1)∩(h=УK))) +
+ Х2(Р((x=Х2)∩(h=У1)) + Р((x=Х2)∩(h=У2)) +¼ + Р((x=Х2)∩(h=УK))) +¼ +
+ ХN(Р((x=ХN)∩(h=У1)) + Р((x=ХN)∩(h=У2)) +¼ + Р((x=ХN)∩(h=УK))) +
+ У1(Р((x=Х1)∩(h=У1)) + Р((x=Х2)∩(h=У1)) +¼ + Р((x=ХN)∩(h=У1))) +
+ У2(Р((x=Х1)∩(h=У2)) + Р((x=Х2)∩(h=У2)) +¼ + Р((x=ХN)∩(h=У2))) + ¼
+ УK(Р((x=Х1)∩(h=УK)) + Р((x=Х2)∩(h=УK)) +¼ + Р((x=ХN)∩(h=УK))) =
= Х1Р(x=Х1) + Х2Р(x=Х2) +¼+ ХN Р(x=ХN) +
+ У1Р(h=У1) + У2Р(h=У2) +¼+ У1Р(h=У1) = MX + MH
При выводе этой формулы использован очевидный факт, что, например, событие x=Х1 можно представить в виде объединения несовместных событий (x=Х1)∩(h=У1), (x=Х1)∩(h=У2), ¼, (x=Х1)∩(h=УN).
Пример.
Заданы N Одинаково распределённых случайных величин x1, x2, ¼, xN с законом распределения
|
XI |
1 |
0 |
|
P |
P |
Q |
Найти математическое ожидание суммы этих случайных величин.
M(![]() ) =
) = 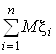 = Np
= Np
Теорема.
Если случайные величины x и h независимы, то
М(xh) = МX×МH
Доказательство.
Если заданы законы распределения двух независимых случайных величин x и h
|
X |
Х1 |
¼ |
Xi |
¼ |
XN |
H |
Y1 |
¼ |
Yj |
¼ |
Yk | |
|
Р |
|
¼ |
|
¼ |
|
Р |
|
¼ |
|
¼ |
|
То математическое ожидание произведения этих случайных величин можно представить следующим образом:
М(xh) = 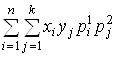 =
=
= Х1![]()
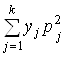 +Х2
+Х2![]()
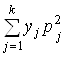 +¼+ ХI
+¼+ ХI![]()
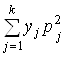 ¼+ ХN
¼+ ХN![]()
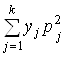 =
=
= Х1![]() MH + Х2
MH + Х2![]() MH + ¼+ ХI
MH + ¼+ ХI![]() MH¼+ ХN
MH¼+ ХN![]() MH = MH
MH = MH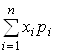 = МX×МH
= МX×МH
| < Предыдущая | Следующая > |
|---|