10. Распределение Стьюдента
Многие задачи статистики приводят к случайной величине вида
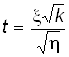 ,
,
Где x и h – независимые случайные величины, причем x – нормально распределенная случайная величина с параметрами MX = 0 и DX = 1, а h распределена по закону c2 c K степенями свободы.
Закон распределения случайной величины T Называется Законом Распределения Стьюдента с K Степенями свободы.
График плотности распределения для закона Стьюдента схематически изображен на рисунке 3. Кривая плотности распределения схожа с аналогичной кривой для нормального распределения.
Таблицы распределения Стьюдента позволяют при данном числе степеней свободы K по вероятности Q определить значение Tq, для которого выполняется соотношение P(|T| > Tq) = Q. Фрагмент такой таблицы представляет собой таблица 2.
|
Q K |
0,1 |
0,05 |
... |
0,01 |
0,005 |
... |
|
1 |
6,314 |
12,71 |
... |
63,57 |
318 |
... |
|
... |
... |
... |
... |
... |
... |
... |
|
12 |
1,782 |
2,179 |
... |
3,055 |
3,428 |
... |
|
... |
... |
... |
... |
... |
... |
... |
|
Таблица 2 |
Задача. Найти симметричный интервал, в который случайная величина, распределенная по закону Стьюдента с 12-ю степенями свободы, попадает вероятностью 0,9.
Решение. Очевидны соотношения:
P(–X < T < X) = P(|T| < X) = 1 – P(|T| ³ X) = 0,9.
Из последнего равенства следует:
P(|T| ³ X) = 0,1 , (N = 12).
Определяем из таблицы: X = 1,782. Нестрогое неравенство в скобках в левой части последней формулы нас не должно смущать, так как мы имеем дело с непрерывной случайной величиной, и вероятность того, что она примет конкретное значение, равна нулю.
Задача. Найти значение X Из условия P(T > X) = 0,995 , где T – случайная величина, распределенная по закону Стьюдента с 12-ю степенями свободы.
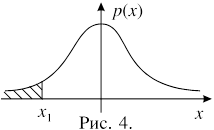
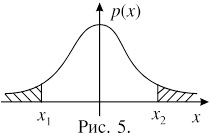
Решение. На рисунке 4 изображен график плотности распределения Стьюдента с 12-ю степенями свободы. Вероятность того, что случайная величина примет значение из области справа от точки X1 равна 0,995 , следовательно в область левее этой точки случайная величина попадает с вероятностью 0,005. Чтобы найти X1, рассмотрим две симметричные области, изображенные на рисунке 5. Допустим, что в каждой из этих областей значение случайной величины оказывается с вероятностью 0,005. Тогда получаем: X1= – x,
X2 = X, причем X определяется из условия
P(|T| > X) = 0,01. Из таблицы 2 находим: X = 3,055. Теперь можно выписать ответ задачи:
P(T > –3,055) = 0,995.
| < Предыдущая | Следующая > |
|---|