09. Распределение хи квадрат
Пусть имеется N независимых случайных величин x1, x2, ..., xn, распределенных по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной единице. Тогда случайная величина ![]() распределена по закону, который называется “распределение c2” или “распределение Пирсона”. Очевидно, что она может принимать лишь неотрицательные значения. Число N называется Числом степеней свободы.
распределена по закону, который называется “распределение c2” или “распределение Пирсона”. Очевидно, что она может принимать лишь неотрицательные значения. Число N называется Числом степеней свободы.
При N > 1 график плотности распределения случайной величины c2 представляет собой кривую, изображенную на рисунке 1.
Для того, чтобы определить вероятность попадания случайной величины c2 в какой-либо промежуток из множества положительных чисел, пользуются таблицей распределения c2. Обычно такая таблица позволяет
|
Q N |
0,99 |
0,975 |
0,95 |
... |
0,1 |
0,05 |
0,01 |
|
1 |
0,0315 |
0,0398 |
0,0239 |
... |
2,71 |
3,84 |
6,63 |
|
... |
... |
... |
... |
... |
... |
... |
... |
|
10 |
2,56 |
3,25 |
3,94 |
... |
16,0 |
18,3 |
23,2 |
|
... |
... |
... |
... |
... |
... |
... |
... |
Таблица 1.
По вероятности Q и по числу степеней свободы N Определить так называемый Квантиль CQ2, если Q и cQ2 связаны соотношением
P(c2 > cQ2) = Q.
Эта формула означает: вероятность того, что случайная величина c2 примет значение, большее чем определенное значение cQ2, равна Q.
Таблица 1 представляет собой фрагмент таблицы распределения c2. Из него видно, что случайная величина c2 с 10-ю степенями свободы с вероятностью Q = 0,95 принимает значение, большее 3,94, а та же величина с одной степенью свободы с вероятностью Q = 0,975 превышает 0,00098.
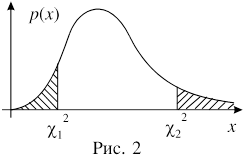
Задача. Найти интервал (c12, c22), в который случайная величина c2 с 10-ю степенями свободы попадает с вероятностью, равной 0,9.
Решение. График плотности распределения c2 с 10-ю степенями свободы схематично изображен на рисунке 2. Будем считать, что площади заштрихованных областей (правая область не ограничена справа) равны между собой. Примем условия:
P(c2 < c12) = P(c2 > c22) = (1 - 0,9)/2 = 0,05, (1)
Тогда P(c12 < c2 < c22) = 0,9.
Равенства (1) сразу позволяют по таблице определить: c22 = 18,3. Для определения левой границы интересующего нас интервала придется воспользоваться очевидным равенством P(c2 > c12) = 0,95. Из таблицы 1. определяем: c12 = 3,94 , и теперь можно сформулировать ответ задачи: значение случайной величины c2 с вероятностью 0,9 принадлежит интервалу (3,94; 18,3).
| < Предыдущая | Следующая > |
|---|