08. Доверительный интервал для дисперсии нормального распределения

Пусть случайная величина X распределена по нормальному закону, для которого дисперсия DX неизвестна. Делается выборка объема N . Из нее определяется исправленная выборочная дисперсия S2. Случайная величина

Распределена по закону C2 c N –1 степенями свободы. По заданной надежности G можно найти сколько угодно границ C12 и C22 интервалов, таких, что

(*)

Найдем C12 и C22 из следующих условий:

P(C2 £ C12) = (1 – G )/ 2 (**)

P(C2 ³ C22) = (1 – G )/ 2 (***)

Очевидно, что при выполнении двух последних условий справедливо равенство (*).

В таблицах для случайной величины C2 обычно дается решение уравнения P(C2 ³CQ2) = Q . Из такой таблицы по заданной величине Q и по числу степеней свободы N – 1 можно определить значение CQ2. Таким образом, сразу находится значение C22 в формуле (***).

Для определения C12 преобразуем (**):

P(C2 ³ C12) = 1 – (1 – G )/ 2 = (1 + G )/ 2

Полученное равенство позволяет определить по таблице значение C12.

Теперь, когда найдены значения C12 и C22, представим равенство (*) в виде

.

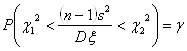Последнее равенство перепишем в такой форме, чтобы были определены границы доверительного интервала для неизвестной
величины DX:

.

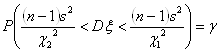Отсюда легко получить формулу, по которой находится доверительный интервал для стандартного отклонения:

(****)

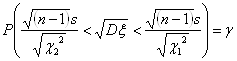Задача. Будем считать, что шум в кабинах вертолетов одного и того же типа при работающих в определенном режиме двигателях — случайная величина, распределенная по нормальному закону. Было случайным образом выбрано 20 вертолетов, и произведены замеры уровня шума (в децибелах) в каждом из них. Исправленная выборочная дисперсия измерений оказалась равной 22,5. Найти доверительный интервал, накрывающий неизвестное стандартное отклонение величины шума в кабинах вертолетов данного типа с надежностью 98%.

Решение. По числу степеней свободы, равному 19, и по вероятности (1 – 0,98)/2 = 0,01 находим из таблицы распределения C2 величину
C22 = 36,2. Аналогичным образом при вероятности (1 + 0,98)/2 = 0,99 получаем C12 = 7,63. Используя формулу (****), получаем искомый доверительный интервал: (3,44; 7,49).

< Предыдущая		Следующая >