07. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии

Пусть X – Случайная величина, распределенная по нормальному закону с неизвестным математическим ожиданием MX, которое обозначим буквой A . Произведем выборку объема N. Определим среднюю выборочную и исправленную выборочную дисперсию S2 по известным формулам.

Случайная величина

Распределена по закону Стьюдента с N – 1 степенями свободы.

Задача заключается в том, чтобы по заданной надежности G и по числу степеней свободы N – 1 Найти такое число TG , чтобы выполнялось равенство

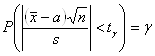(2)

Или эквивалентное равенство

(3)

Здесь в скобках написано условие того, что значение неизвестного параметра A принадлежит некоторому промежутку, который и является доверительным интервалом. Его границы зависят от надежности G , а также от параметров выборки и S.

Чтобы определить значение TG по величине G, равенство (2) преобразуем к виду:

Теперь по таблице для случайной величины T, распределенной по закону Стьюдента, по вероятности 1 – G и числу степеней свободы N – 1 находим TG . Формула (3) дает ответ поставленной задачи.

Задача. На контрольных испытаниях 20-ти электроламп средняя продолжительность их работы оказалась равной 2000 часов при среднем квадратическом отклонении (рассчитанном как корень квадратный из исправленной выборочной дисперсии), равном 11-ти часам. Известно, что продолжительность работы лампы является нормально распределенной случайной величиной. Определить с надежностью 0,95 доверительный интервал для математического ожидания этой случайной величины.

Решение. Величина 1 – G в данном случае равна 0,05. По таблице распределения Стьюдента, при числе степеней свободы, равном 19, находим: TG = 2,093. Вычислим теперь точность оценки: 2,093´121/ = 56,6. Отсюда получаем искомый доверительный интервал:

(1943,4; 2056,6).

< Предыдущая		Следующая >