06. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии
Пусть случайная величина X (можно говорить о генеральной совокупности) распределена по нормальному закону, для которого известна дисперсия DX = S 2 (S > 0). Из генеральной совокупности (на множестве объектов которой определена случайная величина) делается выборка объема N. Выборка X1, x2,..., xn рассматривается как совокупность N независимых случайных величин, распределенных так же как X (подход, которому дано объяснение выше по тексту).
Ранее также обсуждались и доказаны следующие равенства:
Mx1 = Mx2 = ... = Mxn = MX;
Dx1 = Dx2 = ... = Dxn = DX;
![]() MX;
MX;
![]() DX /N;
DX /N;
Достаточно просто доказать (мы доказательство опускаем), что случайная величина ![]() в данном случае также распределена по нормальному закону.
в данном случае также распределена по нормальному закону.
Обозначим неизвестную величину MX через A и подберем по заданной надежности G число D > 0 так, чтобы выполнялось условие:
P(|![]() – A| < D) = G (1)
– A| < D) = G (1)
Так как случайная величина ![]() распределена по нормальному закону с математическим ожиданием M
распределена по нормальному закону с математическим ожиданием M![]() = MX = A И дисперсией D
= MX = A И дисперсией D![]() = DX /n = S 2/n, получаем:
= DX /n = S 2/n, получаем:
P(|![]() – A| < D) =P(A – d <
– A| < D) =P(A – d < ![]() < A + D) =
< A + D) =
= 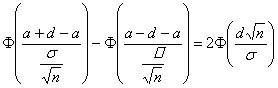
Осталось подобрать D таким, чтобы выполнялось равенство 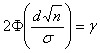 или
или 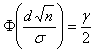 .
.
Для любого G Î[0;1] можно по таблице найти такое число T, что
F( t )= G / 2. Это число T Иногда называют Квантилем.
Теперь из равенства
![]()
Определим значение D: ![]() .
.
Окончательный результат получим, представив формулу (1) в виде:
![]() .
.
Смысл последней формулы состоит в следующем: с надежностью G доверительный интервал
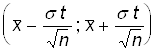
Покрывает неизвестный параметр A = MX генеральной совокупности. Можно сказать иначе: точечная оценка ![]() определяет значение параметра MX с точностью D=S t /
определяет значение параметра MX с точностью D=S t /![]() И надежностью g.
И надежностью g.
Задача. Пусть имеется генеральная совокупность с некоторой характеристикой, распределенной по нормальному закону с дисперсией, равной 6,25. Произведена выборка объема N = 27 и получено средневыборочное значение характеристики ![]() = 12. Найти доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с надежностью G =0,99.
= 12. Найти доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с надежностью G =0,99.
Решение. Сначала по таблице для функции Лапласа найдем значение T Из равенства F (T) = G / 2 = 0,495. По полученному значению
T = 2,58 определим точность оценки (или половину длины доверительного интервала) D: D = 2,5´2,58 / ![]() » 1,24. Отсюда получаем искомый доверительный интервал: (10,76; 13,24).
» 1,24. Отсюда получаем искомый доверительный интервал: (10,76; 13,24).
| < Предыдущая | Следующая > |
|---|